已知x满足不等式(log2x)2+7log2x+6≤0,求函数f(x)=(log24x)•(log42x)的值域.
分析:把“对数log2x”作为一个整体,求不等式(log2x)2+7log2x+6≤0的解集,即求出log2x的范围,利用对数的运算性质和换低公式,化简函数的解析式,再把“对数log2x”作为一个整体利用配方法进行化简,由log2x的范围和二次函数的性质,求出函数的值域.
解答:解:由题意知:(log
2x)
2+7log
2x+6≤0,解得-6≤log
2x≤-1
∵f(x)=(log
24x)•(log
42x)=(log
24+log
2x)(
log
22+
log
2x)
=
(log22x+3log2x+2),
∴
f(x)=[log22x+3log2x+2]=
[log2x+]2-,
由-6≤log
2x≤-1得:
0≤(log2x+)2≤,
∴当log
2x=
-时,f(x)有最小值是
-;当log
2x=-6时,f(x)有最大值是10,
∴
-≤f(x)≤10,
∴f(x)的值域是
[-,10].
点评:本题考查了求对数型复合函数的值域,把“对数log2x”作为一个整体,求它的范围,利用对数的运算把函数转化为关于它的二次函数,利用二次函数的性质求函数的值域,考查了整体思想和转化思想.



 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) B、
B、
 D、m,n的关系不能确定
D、m,n的关系不能确定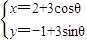 (θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .
(θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .