已知数列{an}满足:a1=2,an+1=3an+2;数列{bn},其中bn=an+1.
(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn;
(3)设cn=(2n-1)bn,求数列{cn}的前n项和Tn.
解:(1)由a
n+1=3a
n+2得,a
n+1+1=3(a
n+1),
所以{a
n+1}为以a
1+1为首项、3为公比的等比数列,
所以a
n+1=3•3
n-1=3
n,
故a
n=3
n-1;
(2)由(1)得,S
n=a
1+a
2+…+a
n=(3-1)+(3
2-1)+…+(3
n-1)
=(3+3
2+…+3
n)-n
=
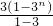
-n=
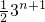
-n-

;
(3)b
n=a
n+1=3
n,所以c
n=(2n-1)b
n=(2n-1)3
n,
所以T
n=1•3+3•3
2+…+(2n-1)3
n①,
3T
n=1•3
2+3•3
3+…+(2n-1)3
n+1②,
①-②得,-2T
n=3+2•3
2+2•3
3+…+2•3
n-(2n-1)•3
n+1
=3+
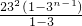
-(2n-1)•3
n+1=2(1-n)•3
n+1-6,
所以T
n=(n-1)•3
n+1+3.
分析:(1)由a
n+1=3a
n+2得,a
n+1+1=3(a
n+1),可判断{a
n+1}为等比数列,可求得a
n+1,进而可得a
n;
(2)分组后分别用等比数列、等差数列求和公式即可求得S
n;
(3)由(1)先求得b
n,进而可得c
n,利用错位相减法即可求得T
n.
点评:本题考查递推公式、等差数列与等比数列的综合及数列求和问题,考查错位相减法求数列的前n项和,属中档题.

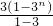 -n=
-n=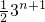 -n-
-n- ;
;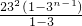 -(2n-1)•3n+1=2(1-n)•3n+1-6,
-(2n-1)•3n+1=2(1-n)•3n+1-6,
