
已知函数
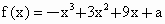 .
.
(1)
求f(x)的单调递减区间;(2)
若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.(2005
·北京)|
(1)∵ ∴ 函数f(x)的单调递减区间为(-∞,-1),(3,+∞).(2)∵f( -2)=8+12-18+a=2+a,f(2)=-8+12+18+a=22+a ∴f(2)>f(-2). 于是有22+a=20,∴a=-2. ∴ ∵ 在(-1,3)上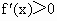 ,∴f(x)在[-1,2]上单调递增. ,∴f(x)在[-1,2]上单调递增.
又由于 f(x)在[-2,-1]上单调递减,∴f(2) 和f(-1)分别是f(x)在区间[-2,2]上的最大值和最小值.∴f( -1)=1+3-9-2=-7.即函数 f(x)在区间[-2,2]上的最小值为-7. |
|
解析:本题主要考查利用导数求函数的单调区间及最值的方法.第 (1)小题应先求 |


科目:高中数学 来源:2013-2014学年山东省济南市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)若 ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)当 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由;
(3)求证:当 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省汕头市高三毕业班教学质量检测文科数学(含解析) 题型:解答题
(本题满分14分)
已知函数 ,
,
(1)求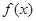 的最小值;
的最小值;
(2)若对所有 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com