
| A. | a7 | B. | a8 | C. | a9 | D. | a10 |
分析 由${S}_{15}=\frac{15({a}_{1}+{a}_{15})}{2}$>0,得a8>0,由${S}_{16}=\frac{15({a}_{1}+{a}_{16})}{2}=\frac{15}{2}({a}_{8}+{a}_{9})<0$,得a8+a9<0,由此能求出在数列{an}中绝对值最小的项.
解答 解:∵等差数列{an}的前n项的和为Sn,S15>0,S16<0,
∴${S}_{15}=\frac{15({a}_{1}+{a}_{15})}{2}$=$\frac{30{a}_{8}}{2}$>0,∴a8>0,
∵${S}_{16}=\frac{15({a}_{1}+{a}_{16})}{2}=\frac{15}{2}({a}_{8}+{a}_{9})<0$,
∴a8+a9<0,∴a9<0,
∴数列{an}为减列,且a1>a2>…>a8>0>a9>a10>…,
∵∴a8+a9<0,∴|a8|<|a9|,
∴在数列{an}中绝对值最小的项为a8.
故选:B.
点评 本题考查等差数列中绝对值最小的项的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
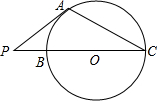 如图,已知PA与圆O相切于点A,经过圆心O的割线PBC交圆O于点B,C,AC=AP,则$\frac{PC}{AC}$的值为( )
如图,已知PA与圆O相切于点A,经过圆心O的割线PBC交圆O于点B,C,AC=AP,则$\frac{PC}{AC}$的值为( )| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3,7 | B. | 3,5 | C. | 5,7 | D. | 2$\sqrt{2}$,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
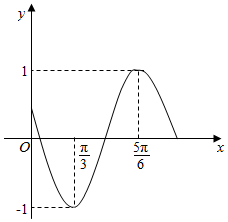 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象,如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
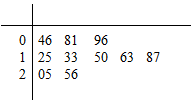 某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:
某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:| 分组 | A | B | C |
| 用电量 | (0,80] | (80,250] | (250,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com