
分析 (1)根据平面向量的坐标运算进行计算即可;
(2)根据单位向量与数量积的定义,计算即可.
解答 解:(1)$\overrightarrow a$=(2,1),$\overrightarrow b$=(-3,4),
∴$\overrightarrow a$+$\overrightarrow b$=(2-3,1+4)=(-1,5),
$\overrightarrow a$-$\overrightarrow b$=(2+3,1-4)=(5,-3),
3$\overrightarrow a$+4$\overrightarrow b$=(3×2-4×3,3×1+4×4)=(-6,19);
(2)∵单位向量$\overrightarrow{e_1}$,$\overrightarrow{e_2}$的夹角为60°,
∴$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=1×1×cos60°=$\frac{1}{2}$;
又$\overrightarrow a$=$\overrightarrow{e_1}$+$\overrightarrow{e_2}$,$\overrightarrow b$=$\overrightarrow{e_2}$-2$\overrightarrow{e_1}$,
∴$\overrightarrow a•\overrightarrow b$=$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$-2${\overrightarrow{{e}_{1}}}^{2}$+${\overrightarrow{{e}_{2}}}^{2}$-2$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$
=$\frac{1}{2}$-2+1-2×$\frac{1}{2}$
=-$\frac{3}{2}$.
点评 本题考查了平面向量的坐标运算与数量积运算问题,是基础题目.


科目:高中数学 来源: 题型:解答题
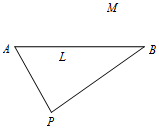 我边防局接到情报,在海礁AB所在直线l的一侧点M处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕.如图,已知快艇出发位置在l的另一侧码头P处,PA=8公里,PB=10公里,∠APB=60°.
我边防局接到情报,在海礁AB所在直线l的一侧点M处有走私团伙在进行交易活动,边防局迅速派出快艇前去搜捕.如图,已知快艇出发位置在l的另一侧码头P处,PA=8公里,PB=10公里,∠APB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 打球年限x/年 | 3 | 5 | 6 | 7 | 9 |
| 投中球数y/个 | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≥2015 | B. | ?x∈R,x2<2015 | C. | ?x∈R,x2≥2015 | D. | ?x∈R,x2>2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$3 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
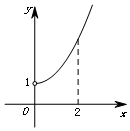 已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )
已知函数y=f(x)(x∈R)是奇函数,其部分图象如图所示,则在(-2,0)上与函数f(x)的单调性相同的是( )| A. | y=x2+1 | B. | y=log2|x| | ||
| C. | y=$\left\{\begin{array}{l}{{e}^{x}(x≥0)}\\{{e}^{-x}(x<0)}\end{array}\right.$ | D. | y=|x+2| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M=N | B. | M⊆N | ||
| C. | N⊆M | D. | M,N不存在包含关系 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com