设F
1、F
2为曲线C
1:
+
=1的焦点,P是曲线C
2:
-y
2=1与C
1的一个交点,则△PF
1F
2的面积为
.
分析:根据双曲线和椭圆的定义可得 PF
1+PF
2=2
,PF
1-PF
2=2
,△PF
1F
2 中,由余弦定理可得
cos∠F
1PF
2=
,故 sin∠F
1PF
2=
,由△PF
1F
2的面积为
•PF
1•PF
2•sin∠F
1PF
2运算
得到结果.
解答:解:由曲线C
1:
+
=1的方程可得 F
1 (-2,0)、F
2 (2,0),再由椭圆的定义可得
PF
1+PF
2=2
. 又因曲线C
2:
-y
2=1 的焦点和曲线C
1 的焦点相同,再由双曲线的定义可得
PF
1-PF
2=2
.∴PF
1=
+ ,PF
2=
-.
△PF
1F
2 中,由余弦定理可得 16=
(+)2+ (-)2-2(
+)(
-)cos∠F
1PF
2 ,
解得 cos∠F
1PF
2=
,∴sin∠F
1PF
2=
,
△PF
1F
2的面积为
•PF
1•PF
2•sin∠F
1PF
2=
(
+ )(
-)sin∠F
1PF
2=
,
故答案为:
.
点评:本题考查双曲线和椭圆的定义和标准方程,以及简单性质的应用,求出 PF
1=
+ ,PF
2=
-,
sin∠F
1PF
2 的值,是解题的关键.
练习册系列答案
相关习题
科目:高中数学
来源:湖南邵东二中2008届高三质量检测数学试题卷
题型:013
查看答案和解析>>
科目:高中数学
来源:2010年浙江省杭州市七校联考高二下学期期中考试数学(理)
题型:选择题
设F1、F2为曲线C1: 的焦点,P是曲线
的焦点,P是曲线 :
: 与C1的一个交点,
与C1的一个交点,
则△PF1F2的面积为
( )
A. B. 1 C.
D.
2
查看答案和解析>>
科目:高中数学
来源:2010-2011学年北京四中高二(上)期中数学试卷(文科)(解析版)
题型:选择题
设F
1,F
2为曲线C
1:
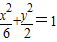
的焦点,P是曲线C
2:
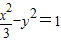
与C
1的一个交点,则
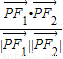
的值为( )
A.

B.

C.

D.-

查看答案和解析>>
科目:高中数学
来源:2005年北京四中高考数学二模试卷(理科)(解析版)
题型:选择题
设F
1,F
2为曲线C
1:
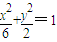
的焦点,P是曲线C
2:
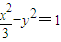
与C
1的一个交点,则
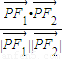
的值为( )
A.

B.

C.

D.-

查看答案和解析>>
科目:高中数学
来源:2006-2007学年江苏省泰州市姜堰中学高三(下)4月月考数学试卷(解析版)
题型:选择题
设F
1,F
2为曲线C
1:
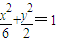
的焦点,P是曲线C
2:
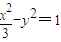
与C
1的一个交点,则
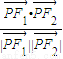
的值为( )
A.

B.

C.

D.-

查看答案和解析>>



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案![]() 的焦点,P是曲线C2:
的焦点,P是曲线C2:![]() 与C1的一个交点,则
与C1的一个交点,则 的值为
的值为![]()
![]()
![]()
![]()
 的焦点,P是曲线
的焦点,P是曲线 :
: 与C1的一个交点,
与C1的一个交点,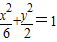 的焦点,P是曲线C2:
的焦点,P是曲线C2: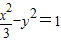 与C1的一个交点,则
与C1的一个交点,则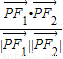 的值为( )
的值为( )



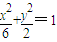 的焦点,P是曲线C2:
的焦点,P是曲线C2: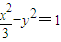 与C1的一个交点,则
与C1的一个交点,则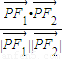 的值为( )
的值为( )



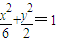 的焦点,P是曲线C2:
的焦点,P是曲线C2: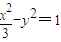 与C1的一个交点,则
与C1的一个交点,则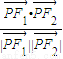 的值为( )
的值为( )


