
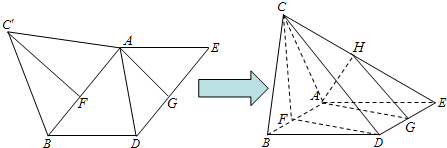
 ,AB,DE的中点分别为F,G.现沿直线AB将△ABC'翻折成△ABC,使二面角C-AB-D为120°,设CE中点为H.
,AB,DE的中点分别为F,G.现沿直线AB将△ABC'翻折成△ABC,使二面角C-AB-D为120°,设CE中点为H.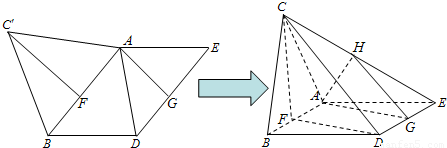
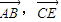 的坐标,利用向量的夹角公式,即可求异面直线AB与CE所成角的正切值;
的坐标,利用向量的夹角公式,即可求异面直线AB与CE所成角的正切值;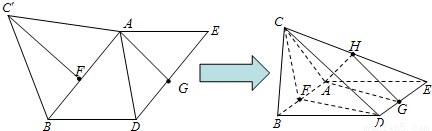 解法一:(Ⅰ) (i)证明:连FD.因为ABDE为平行四边形,F、G分别为AB、DE中点,
解法一:(Ⅰ) (i)证明:连FD.因为ABDE为平行四边形,F、G分别为AB、DE中点,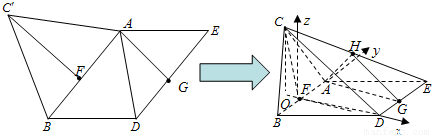
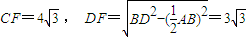 ,
,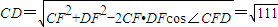 ,
,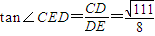 .---------------------(9分)
.---------------------(9分)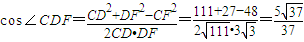 .---------------(14分)
.---------------(14分)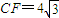 得
得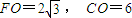 .--------(6分)
.--------(6分)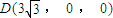 ,
, ,
,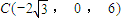 ,
, ,
,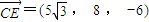 .----------------(8分)
.----------------(8分) ,
, .------------------------------(10分)
.------------------------------(10分)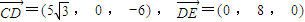 ,
, =(x,y,z),则由
=(x,y,z),则由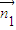 ⊥
⊥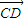 ,
,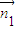 ⊥
⊥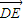 得
得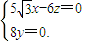
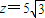 ,得
,得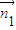 =
=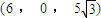 .-----------(12分)
.-----------(12分)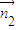 =(0,0,1),而二面角C-DE-F为锐二面角,
=(0,0,1),而二面角C-DE-F为锐二面角,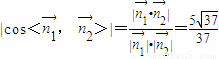 .-------------(14分)
.-------------(14分)

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
| 43 |
查看答案和解析>>
科目:高中数学 来源:2007届武穴中学高三文科数学模拟题 题型:044
如图,把正△ABC分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第1行,…,BC为第n行,记点A上的数为a11,…第i行中左起第j个数为aij(1≤j≤i)若a11=1,![]()
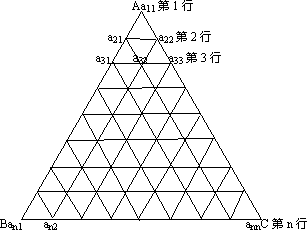
(1)求a31,a32,a33;
(2)试归纳出anm的表达式(用含n,m的式子表示,不必证明);
(3)记S=an1+an2+…+ann,证明![]()
查看答案和解析>>
科目:高中数学 来源:湖北省武穴2007届文科数学模拟题 题型:044
如图,把正△ABC分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第1行,…,BC为第n行,记点A上的数为a11,…,第i行中左起第j个数为aij(1≤j≤i).若![]()
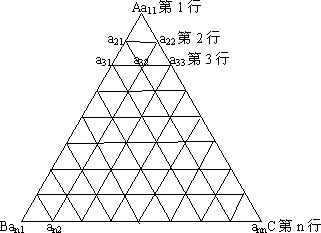
(1)求a31,a32,a33;
(2)试归纳出anm的表达式(用含n,m的式子表示,不必证明);
(3)记S=an1+an2+…+ann,证明![]()
查看答案和解析>>
科目:高中数学 来源:训练必修二数学苏教版 苏教版 题型:013
如图,一个正三棱柱形容器中盛有水,且侧棱AA1=8,若侧面AA1B1B水平放置时,液面恰好过AC、BC、A1C1、B1C1的中点.当底面ABC水平放置时,液面高为
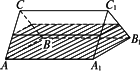
A.4
B.6
C.![]()
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com