
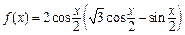 .
.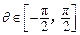 ,且
,且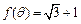 ,求
,求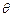 的值;
的值;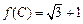 ,且△ABC的面积为
,且△ABC的面积为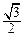 ,求sinA+sinB的值.
,求sinA+sinB的值.科目:高中数学 来源:不详 题型:解答题
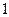 ,圆心角为
,圆心角为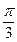 的扇形木板
的扇形木板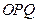 ,现要用其截出一块面积最大的矩形木板,下面提供了两种截出方案,试比较两种方案截出的最大矩形面积哪个最大?请说明理由。
,现要用其截出一块面积最大的矩形木板,下面提供了两种截出方案,试比较两种方案截出的最大矩形面积哪个最大?请说明理由。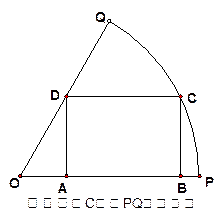
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
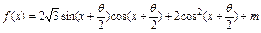 ,(其中
,(其中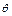 ,
,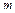 为常数,
为常数,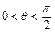 )图象的一个对称中心是
)图象的一个对称中心是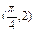 .
.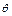 和
和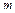 的值;
的值;
|
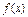 的单调递减区间;(III)求满足
的单调递减区间;(III)求满足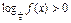 的
的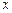 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
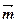 =(sin2x,cosx),
=(sin2x,cosx), =(
=(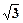 ,2cosx)(x∈R),f(x)=
,2cosx)(x∈R),f(x)=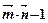
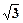 ,B=
,B=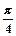 ,求b的值。
,求b的值。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com