
分析 由已知中函数$f(x)=\left\{\begin{array}{l}-{x}^{2}+1,x≤1\\ x-1,x>1\end{array}\right.$,分类讨论满足方程f(a+1)=f(a)的实数a的值,综合可得答案.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}-{x}^{2}+1,x≤1\\ x-1,x>1\end{array}\right.$,f(a+1)=f(a)
当a≤-1或a≥1,时f(a+1)≠f(a);
当-1<a<0,即0<a+1<1时,由f(a+1)=f(a)得-(a+1)2+1=-a2+1,
解得$a=-\frac{1}{2}$;
当a=0,即a+1=1时,f(a+1)=0≠f(a)=1;
当0<a<1即1<a+1<2时,由f(a+1)=f(a)得(a+1)-1=-a2+1,
解得$a=\frac{{-1+\sqrt{5}}}{2}$,$a=\frac{{-1-\sqrt{5}}}{2}$(舍去);
综上:$a=-\frac{1}{2}$或$a=\frac{{-1+\sqrt{5}}}{2}$.
故答案为:-$\frac{1}{2}$,或$\frac{-1+\sqrt{5}}{2}$
点评 本题考查的知识点是分段函数的应用,函数求值,分类讨论思想,难度中档.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 幂函数 | B. | 对数函数 | C. | 指数函数 | D. | 余弦函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列说法中正确的个数为( )
如图正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列说法中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
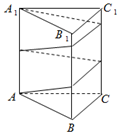 已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为4cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )
已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为4cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为( )| A. | 4$\sqrt{10}$cm | B. | 12$\sqrt{3}$cm | C. | 2$\sqrt{13}$cm | D. | 13cm |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com