A
分析:将函数看作是复合函数,令g(x)=x
3-2ax+2a-1,将函数f(x)的单调性问题转化为g(x)恒大于零且g′(x)恒正、恒负问题,通过分类讨论,解决不等式恒成立问题即可得a的范围
解答:设g(x)=x
3-2ax+2a-1=(x-1)(x
2+x+1-2a),g′(x)=3x
2-2a
当a∈(0,1)时,函数

内单调递增,等价于g(x)在区间(-

,0)内单调递减且g(x)>0在区间(-

,0)内恒成立
∴g′(x)≤0在区间(-

,0)内恒成立且g(x)>0在区间(-

,0)内恒成立
∴3x
2-2a≤0恒成立且g(0)≥0
只需

,解得a≥

,∴

≤a<1
当a∈(1,+∞)时,函数

内单调递增,等价于g(x)在区间(-

,0)内单调递增且g(x)>0在区间(-

,0)内恒成立
∴g′(x)≥0在区间(-

,0)内恒成立且g(x)>0在区间(-

,0)内恒成立
∴3x
2-2a≥0恒成立且g(-

)≥0
由于x=0时,3x
2-2a=-2a<0,故上式不可能恒成立,故a∈(1,+∞)不合题意
综上所述:

≤a<1
故选A
点评:本题主要考查复合函数的单调性的判断和应用,对数函数的性质,分类讨论和转化化归的思想方法,解题时一定要注意函数的定义域.

 内单调递增,则a的取值范围
内单调递增,则a的取值范围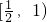



 内单调递增,等价于g(x)在区间(-
内单调递增,等价于g(x)在区间(- ,0)内单调递减且g(x)>0在区间(-
,0)内单调递减且g(x)>0在区间(- ,0)内恒成立
,0)内恒成立 ,0)内恒成立且g(x)>0在区间(-
,0)内恒成立且g(x)>0在区间(- ,0)内恒成立
,0)内恒成立 ,解得a≥
,解得a≥ ,∴
,∴ ≤a<1
≤a<1 内单调递增,等价于g(x)在区间(-
内单调递增,等价于g(x)在区间(- ,0)内单调递增且g(x)>0在区间(-
,0)内单调递增且g(x)>0在区间(- ,0)内恒成立
,0)内恒成立 ,0)内恒成立且g(x)>0在区间(-
,0)内恒成立且g(x)>0在区间(- ,0)内恒成立
,0)内恒成立 )≥0
)≥0 ≤a<1
≤a<1

 名校课堂系列答案
名校课堂系列答案