
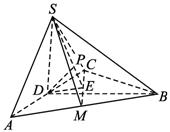
(1)证明:AC⊥SB.
(2)求二面角S—CM—A的大小.
(3)求点B到平面SCM的距离.
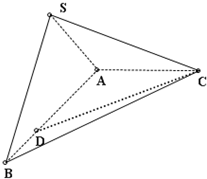
解法一:(1)如图,取AC中点D,连结DS、DB.

∵SA=SC,BA=BC,
∴AC⊥DS且AC⊥DB,
∴AC⊥平面SDB,
又SB![]() 平面SDB,
平面SDB,
∴AC⊥SB.
(2)∵SD⊥AC,平面SAC⊥平面ABC,
∴SD⊥平面ABC.
过D作DE⊥CM于E,连结SE,
则SE⊥CM,
∴∠SED为二面角S—CM—A的平面角.
由已知有DE![]()
![]() AM,所以DE=1,
AM,所以DE=1,
又SA=SC=2![]() ,AC=4,∴SD=2.
,AC=4,∴SD=2.
在Rt△SDE中,tan∠SED=![]() =2,
=2,
∴二面角S—CM—A的大小为arctan2.
(3)在Rt△SDE中,SE=![]() ,CM是边长为4的正△ABC的中线,∴CM=2
,CM是边长为4的正△ABC的中线,∴CM=2![]() .
.
∴S△SCM=![]() CM·SE=
CM·SE=![]() ×2
×2![]() ×
×![]() =
=![]() ,
,
设点B到平面SCM的距离为h,
由VB—SCM=VS—CMB,SD⊥平面ABC,
得![]() S△SCM·h=
S△SCM·h=![]() S△CMB·SD,
S△CMB·SD,
∴h=![]() =
=![]() .
.
即点B到平面SCM的距离为![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:
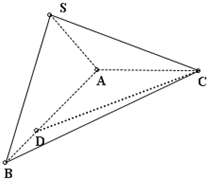 如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1
如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1查看答案和解析>>
科目:高中数学 来源:训练必修二数学人教A版 人教A版 题型:047
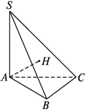
如图所示,在三棱锥S-ABC中,SA⊥底面ABC,底面ABC为正三角形,AH⊥面SBC.求证:H不可能是△SBC的垂心.
查看答案和解析>>
科目:高中数学 来源: 题型:
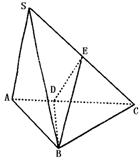 如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com