【题目】已知等差数列{an}满足a4=6，a6=10．
（1）求数列{an}的通项公式；
（2）设等比数列{bn}各项均为正数，其前n项和Tn ， 若b3=a3 ， T2=3，求Tn ．
科目：高中数学 来源： 题型：
【题目】已知两个半径不等的圆盘叠放在一起（有一轴穿过它们的圆心），两圆盘上分别有互相垂直的两条直径将其分为四个区域，小圆盘上所写的实数分别记为x1 ， x2 ， x3 ， x4 ， 大圆盘上所写的实数分别记为y1 ， y2 ， y3 ， y4 ， 如图所示．将小圆盘逆时针旋转i（i=1，2，3，4）次，每次转动90° ， 记Ti（i=1，2，3，4）为转动i次后各区域内两数乘积之和，例如T1=x1y2+x2y3+x3y4+x4y1 ． 若x1+x2+x3+x4＜0，y1+y2+y3+y4＜0，则以下结论正确的是（ ）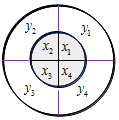 
A.T1 ， T2 ， T3 ， T4中至少有一个为正数
B.T1 ， T2 ， T3 ， T4中至少有一个为负数
C.T1 ， T2 ， T3 ， T4中至多有一个为正数
D.T1 ， T2 ， T3 ， T4中至多有一个为负数
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数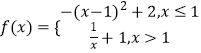 
下列四个命题：
①f(f（1）)>f（3）； ② 
x0∈(1,+∞),f'(x0)=-1/3；
③f(x)的极大值点为x=1； ④ 
x1,x2∈(0,+∞),|f(x1)-f(x2)|≤1
其中正确的有（写出所有正确命题的序号）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=cos（2x﹣ 
）+2cos2x，将函数y=f（x）的图象向右平移 
个单位，得到函数y=g（x）的图象，则函数y=g（x）图象的一个对称中心是（ ）
A.（﹣ 
，1）
B.（﹣ 
，1）
C.（ ，1）
D.（ 
，0）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，曲线C1的参数方程为 
（α为参数，﹣π＜α＜0），曲线C2的参数方程为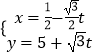 
（t为参数），以O为极点，x轴的正半轴为极轴建立极坐标系．
（1）求曲线C1的极坐标方程和曲线C2的普通方程；
（2）射线θ=﹣ 
与曲线C1的交点为P，与曲线C2的交点为Q，求线段PQ的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线l的参数方程： 
（t为参数），曲线C的参数方程： 
（α为参数），且直线交曲线C于A，B两点．
（Ⅰ）将曲线C的参数方程化为普通方程，并求θ= 
时，|AB|的长度；
（Ⅱ）已知点P：（1，0），求当直线倾斜角θ变化时，|PA||PB|的范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知奇函数y=f（x）定义域是R，当x≥0时，f（x）=x（1﹣x）．
（1）求出函数y=f（x）的解析式；
（2）写出函数y=f（x）的单调递增区间．（不用证明，只需直接写出递增区间即可）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知A、B、C是圆O上的三个点，CO的延长线与线段BA的延长线交于圆外一点．若 
，其中m，n∈R．则m+n的取值范围是（ ）
A.（0，1）
B.（﹣1，0）
C.（1，+∞）
D.（﹣∞，﹣1）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
