Question

（05年重庆卷文）（13分）

如图，在四棱锥P―ABCD中，底面ABCD为矩形，PD⊥底面ABCD，E是AB上

一点，PE⊥EC. 已知求

   （Ⅰ）异面直线PD与EC的距离；

   （Ⅱ）二面角E―PC―D的大小.

 

Answer 1

解析：解法一：

（Ⅰ）因PD⊥底面，故PD⊥DE，又因EC⊥PE，且DE

是PE在面ABCD内的射影，由三垂直线定理的逆定理知

EC⊥DE，因此DE是异面直线PD与EC的公垂线.

设DE=x，因△DAE∽△CED，故（负根舍去）.

从而DE=1，即异面直线PD与EC的距离为1.

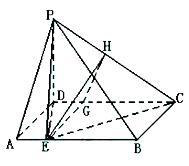
（Ⅱ）过E作EG⊥CD交CD于G，作GH⊥PC交PC于H，连接EH. 因PD⊥底面，

故PD⊥EG，从而EG⊥面PCD.

因GH⊥PC，且GH是EH在面PDC内的射影，由三垂线定理知EH⊥PC.

因此∠EHG为二面角的平面角.

在面PDC中，PD=，CD=2，GC=

因△PDC∽△GHC，故，

又

故在

即二面角E―PC―D的大小为

解法二：

（Ⅰ）以D为原点，、、分别为x、y、

z轴建立空间直角坐标系.

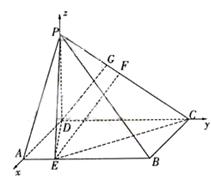
由已知可得D（0，0，0），P（0，0，，

C（0，2，0）设

  由，

即  由，

又PD⊥DE，故DE是异面直线PD与CE的公垂线，易得，故异面直线PD、

CE的距离为1.

（Ⅱ）作DG⊥PC，可设G（0，y，z）.由得

即作EF⊥PC于F，设F（0，m，n），

则

由，

又由F在PC上得

因故平面E―PC―D的平面角的大小为向量的夹角.故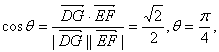  即二面角E―PC―D的大小为