已知函数法(x)=x2+2ax+2.
①若方程f(x)=0有两不相等的正根,求a的取值范围;
②若函数f(x)满足f(x+1)=f(1-x),求函数在x∈[-5,5]的最大值和最小值;
③求f(x)在x∈[-5,5]的最小值.
【答案】
分析:(1)方程f(x)=0有两不相等的正根等价于

,解此不等式组即可.
(2)由f(x+1)=f(1-x)可以求出a=-1,再结合二次函数的图象与性质求解.
(3)对称轴x=-a,分-a<-5,-5≤-a≤5,-a>5三类,结合二次函数的图象与性质求解.
解答:解:(1)设方程x
2+2ax+2=0的两根为x
1,x
2,
则

,解得a
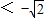
(2)由题意得(x+1)
2+2a(x+1)+2=(1-x)
2+2a(1-x)+2
即4(1+a)x=0对任意x∈R恒成立,
∴a=-1.∴f(x)=x
2-2x+2,x∈[-5,5],
∵f(x)在[-5,1]上单调递减,在[1,5]上单调递增,
∴f(x)的最大值为f(-5)=37,f(x)的最小值为f(1)=1.
(3)对称轴x=-a,
当-a<-5,即a>5时,f(x)在[-5,5]上单调递增,f(x)的最小值为f(-5)=27-10a,
当-5≤-a≤5,即-5≤a≤5时,f(x)在[-5,-a]上单调递减,在[-a,5]上单调递增,
f(x)的最小值为f(-a)=2-a
2.
当-a>5,即a<-5时,f(x)在[-5,5]上单调递减,f(x)的最小值为f(5)=27+10a.
综上:f(x)
min=
 点评:
点评:本题考查二次方程根的分布,二次函数的图象与性质.考查数形结合、分类讨论、计算能力.

 ,解此不等式组即可.
,解此不等式组即可. ,解得a
,解得a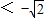



 已知函数f(x)=2sin2(
已知函数f(x)=2sin2(