
已知函数![]() 定义域为
定义域为![]() (
(![]() ),设
),设![]() .
.
(Ⅰ)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,并确定这样的
,并确定这样的![]() 的个数.
的个数.
![]() ,且当
,且当![]() 时,有唯一的
时,有唯一的![]() 适合题意;当
适合题意;当![]() 时,有两个
时,有两个![]() 适合题意
适合题意
【解】 (Ⅰ)解:因为![]() …………………………(2分)
…………………………(2分)
由![]() ;由
;由![]() ,所以
,所以![]() 在
在![]() 上递增,
上递增,
在![]() 上递减 …………………………………………………………………(4分)
上递减 …………………………………………………………………(4分)
欲![]() 在
在![]() 上为单调函数,则
上为单调函数,则![]() ……………………………(5分)
……………………………(5分)
(Ⅱ)证:因为![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,所以
上递减,所以![]() 在
在![]() 处取得极小值
处取得极小值![]() (7分)
(7分)
又![]() ,所以
,所以![]() 在
在![]() 上的最小值为
上的最小值为![]() …………………………(9分)
…………………………(9分)
从而当![]() 时,
时,![]() ,即
,即![]() ………………………(10分)
………………………(10分)
(Ⅲ)证:因为![]() ,所以
,所以![]() 即为
即为![]() ,
,
令![]() ,从而问题转化为证明方程
,从而问题转化为证明方程![]() =0
=0
在![]() 上有解,并讨论解的个数…………………………………………(12分)
上有解,并讨论解的个数…………………………………………(12分)
因为![]() ,
,![]() ,所以
,所以
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上有解,且只有一解 …(13分)
上有解,且只有一解 …(13分)
②当![]() 时,
时,![]() ,但由于
,但由于![]() ,
,
所以![]() 在
在![]() 上有解,且有两解 …………………………………(14分)
上有解,且有两解 …………………………………(14分)
③当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上有且只有一解;
上有且只有一解;
当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上也有且只有一解………………………………(15分)
上也有且只有一解………………………………(15分)
综上所述, 对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,
,
且当![]() 时,有唯一的
时,有唯一的![]() 适合题意;当
适合题意;当![]() 时,有两个
时,有两个![]() 适合题意……(16分)
适合题意……(16分)
(说明:第(Ⅱ)题也可以令![]() ,
,![]() ,然后分情况证明
,然后分情况证明![]() 在其值域内,并讨论直线
在其值域内,并讨论直线![]() 与函数
与函数![]() 的图象的交点个数即可得到相应的
的图象的交点个数即可得到相应的![]() 的个数)
的个数)
w.w.w.k.s.5.u.c.o.


科目:高中数学 来源:2010-2011学年浙江省六校高三4月月考考试数学理卷 题型:选择题
已知函数 定义域为
定义域为 ,且函数
,且函数 在
在 上有两个不同的零点,则
上有两个不同的零点,则 的取值范围是( )
的取值范围是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年宁夏高三第四次月考数学试(理)题 题型:选择题
已知函数定义域为D的函数f(x),如果对x D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+
D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+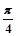 );(3)f(x)=
);(3)f(x)=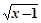 ;(4)f(x)=
;(4)f(x)= ;其中是“倍约束函数”的是( )
;其中是“倍约束函数”的是( )
A.(1)(3)(4) B.(1)(2) C.(3)(4) D.(2)(3)(4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com