
若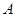 ,
,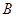 ,
,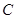 不共线,对于空间任意一点
不共线,对于空间任意一点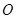 都有
都有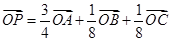 ,则
,则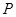 ,
,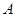 ,
,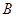 ,
, 四点( )
四点( )
| A.不共面 | B.共面 | C.共线 | D.不共线 |
科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,在多面体ABDEC中,AE 平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
平面ABC,BD//AE,且AC=AB=BC=AE=1,BD=2,F为CD中点。
(I)求证:EF//平面ABC;
(II)求证: 平面BCD;
平面BCD;
(III)求多面体ABDEC的体积。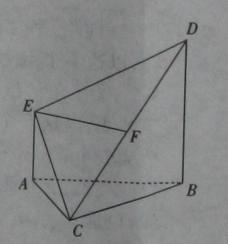
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,在平行六面体ABCD-A1B1C1D1中,底面是边长为1的正方形,若∠A1AB=∠A1AD=60º,且A1A=3,则A1C的长为( )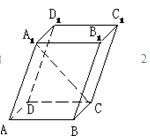
A.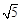 | B.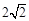 | C.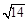 | D.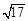 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
[2014·温州质检]△ABC的顶点分别为A(1,-1,2),B(5,-6,2),C(1,3,-1),则AC边上的高BD等于( )
| A.5 | B.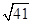 | C.4 | D.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在空间直角坐标系中的点P(a,b,c),有下列叙述:
①点P(a,b,c)关于横轴(x轴)的对称点是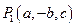 ;
;
②点P(a,b,c)关于yOz坐标平面的对称点为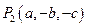 ;
;
③点P(a,b,c)关于纵轴(y轴)的对称点是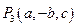 ;
;
④点P(a,b,c)关于坐标原点的对称点为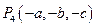 .
.
其中错误的叙述个数是( )
| A.1 |
| B.2 |
| C.3 |
| D.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在空间直角坐标系中,点M的坐标是(4,7,6),则点M关于y轴的对称点在坐标平面xOz上的射影的坐标为( )
| A.(4,0,6) |
| B.(-4,7,-6) |
| C.(-4,0,-6) |
| D.(-4,7,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为( )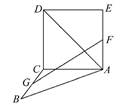
A.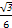 | B.-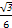 | C.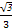 | D.-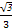 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com