
 ������M��Ӧ�ı任������y=sinx��Ϊ����C����C�ķ��̣�
������M��Ӧ�ı任������y=sinx��Ϊ����C����C�ķ��̣� ��������C����ͨ���̣�
��������C����ͨ���̣�
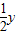 =sin2x���Ӷ���������C�ķ��̣�
=sin2x���Ӷ���������C�ķ��̣�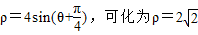 ��sin��+cos�ȣ�������ͬ���Ԧѣ�����ɵ���ͨ���̣�
��sin��+cos�ȣ�������ͬ���Ԧѣ�����ɵ���ͨ���̣� ������5�֣�
������5�֣�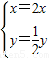 ���ֵ�P��x��y��������y=sinx�ϣ�
���ֵ�P��x��y��������y=sinx�ϣ�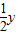 =sin2x��
=sin2x��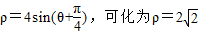 ��sin��+cos�ȣ�������5�֣�
��sin��+cos�ȣ�������5�֣�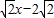 y=0��
y=0��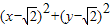 =4������10�֣�
=4������10�֣�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 [ѡ����]������A��B��C��D�ĸ�С����ֻ��ѡ�����⣬ÿС��10�֣���20�֣�
[ѡ����]������A��B��C��D�ĸ�С����ֻ��ѡ�����⣬ÿС��10�֣���20�֣�
|
| �� |
| 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3 |
| 3 |
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ѡ���⣺������������С���У���ѡһ���������ȫ����1С�����֣�
ѡ���⣺������������С���У���ѡһ���������ȫ����1С�����֣�2
| ||
| 3 |
2
| ||
| 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 �����⣺��ѡ���⣺������A��B��C��D�ĸ�С����ֻ��ѡ�����⣩
�����⣺��ѡ���⣺������A��B��C��D�ĸ�С����ֻ��ѡ�����⣩| 5 |
|
|
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011�꽭��ʡ�߿���ѧ����Ѻ���Ծ���01���������棩 ���ͣ������
 �����߶�AC�ij��ȣ�
�����߶�AC�ij��ȣ� ������ֵ��2=2����Ӧ��һ����������
������ֵ��2=2����Ӧ��һ���������� ���������A��
���������A�� �����Dz�����������OΪ���㣬x���������Ϊ���ᣬȡ��ֱ������ϵ����ͬ�ĵ�λ���ȣ�����������ϵ��������C�ļ����귽�̣�
�����Dz�����������OΪ���㣬x���������Ϊ���ᣬȡ��ֱ������ϵ����ͬ�ĵ�λ���ȣ�����������ϵ��������C�ļ����귽�̣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com