Question

在三棱柱ABC-A₁B₁C₁中，AB=BC=CA=AA₁，侧棱AA₁⊥平面ABC，O、D、E分别是棱AB、A₁B₁、AA₁的中点，点F在棱AB上，且AF=

1

4

AB．
（Ⅰ）求证：EF∥平面BDC₁
（Ⅱ）求证：平面OCC₁D⊥平面ABB₁A₁
（Ⅲ）求二面角E-BC₁-D的余弦值．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）连接OA₁，由已知得EF∥OA₁，OBDA₁为平行四边形，从而OA₁∥BD，由此能证明EF∥平面BDC₁．
（Ⅱ）由已知得AA₁⊥OC，OC⊥AB，从而OC⊥平面ABB₁ A₁，由此能证明平面OCC₁D⊥平面ABB₁ A₁．
（Ⅲ）法一：建立空间直角坐标系O-xyz，利用向量法能求出二面角E-BC₁-D的余弦值．
（Ⅲ）法二：CODC₁为平行四边形，从而C₁D∥CO，过E作EG⊥BD于G，过G作GH⊥BC₁于H，连接EH，∠GHE为所求二面角E-BC₁-D的平面角，由此能求出二面角E-BC₁-D余弦值．

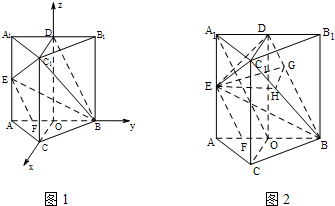
解答： （Ⅰ）证明：如图1，连接OA₁，
O为AB的中点，且AF=

1

4

AB
∴AF=FO，又E为A A₁的中点，
∴EF∥OA₁（2分）
在三棱柱ABC-A₁B₁C₁中，
A₁B₁∥AB且A₁B₁=AB，
∵O、D分别为AB、A₁B₁中点，
∴OB∥A₁D且OB=A₁D，
∴OBDA₁为平行四边形，∴OA₁∥BD（3分）
∴EF∥BD，又EF?平面BDC，BD?平面BDC
∴EF∥平面BDC₁．（4分）
（Ⅱ）证明：如图1，∵AA₁⊥平面ABC，OC?平面ABC，
∴AA₁⊥OC，（5分）
∵AB=BC，O为AB中点
∴OC⊥AB，又AB、AA₁?平面ABB₁ A₁，AB∩AA₁=A（6分）
∴OC⊥平面ABB₁ A₁，又OC?平面OCC₁D
∴平面OCC₁D⊥平面ABB₁ A₁．（8分）
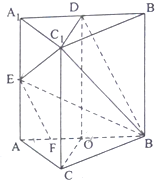
（Ⅲ）解法一，如图2建立空间直角坐标系O-xyz，设AB=2
则A（0，-1，0），A₁（0，-1，2），E（0，-1，1），
C1(

3

，0，2)，B(0，1，0)，D(0，0，2)，（9分）
∴

BC1

=(

3

，-1，2)，

BE

=(0，-2，1)，

BD

=(0，-1，2)
设平面EBC₁的法向量为

n1

=(x1，y1，z1)
则

n1 • BC1 = 3 x1-y1+2z1=0 n1 • BE =-2y1+z1=0

取

n1

=(-

3

，1，2)（10分）
设平面DBC₁的法向量为

n2

=(x2，y2，z2)
则

n2 • BC1 = 3 x2-y2+2z2=0 n2 • BD =-y1+2z1=0

取

n1

=(0，2，1)（11分）
∴cos＜

n1

，

n2

＞=

4

2 2 • 5

=

10

5

故所求二面角E-BC₁-D的余弦值为

10

5

．（12分）
（Ⅲ）解法二，如图1，在三棱柱ABC-A₁B₁C₁中
∵O、D分别为AB、A₁B₁的中点
∴OD平行且等于AA₁，AA₁平行且等于CC₁，
∴CODC₁为平行四边形，
∴C₁D∥CO，由（Ⅱ）知，OC⊥平面ABB₁ A₁
∴C₁D⊥平面ABB₁ A₁
∴面C₁DB⊥平面ABB₁A₁（9分）
过E作EG⊥BD于G，过G作GH⊥B C₁于H，连接EH
∴EG⊥平面BDC₁，EG⊥GH，EG⊥BC₁
∴BC₁⊥平面EGH，BC₁⊥EH，
∴∠GHE为所求二面角E-BC₁-D的平面角（10分）
设AB=2，连接DE，则BE=BD=

5

，DE=

2

，
∴S△BDE=4-

1

2

-1-1=

1

2

•

5

•EG，∴EG=

3 5

5

，BG=

4 5

5

∵

GH

C1D

=

BH

C1B

，又C1D=

3

，C1B=2

2

，∴GH=

30

5

，EH=

3

（11分）
∴cos∠GHE=

GH

EH

=

10

5

，
故所求二面角E-BC₁-D余弦值为

10

5

．（12分）

点评：本题考查直线与平面平行的证明，考查平面与平面垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．