
(本小题14分)
在等差数列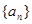 中,
中,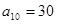 ,
,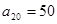 .
.
(1)求数列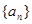 的通项
的通项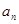 ;
;
(2)令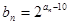 ,证明:数列
,证明:数列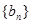 为等比数列;
为等比数列;
(3)求数列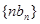 的前
的前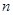 项和
项和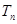 .
.
(1)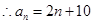 ;
;
(2)见解析
(3) 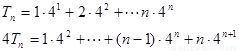
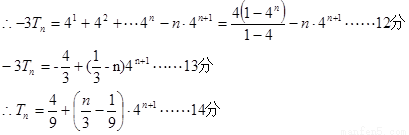
【解析】
试题分析:(1)先由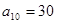 ,
,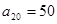 ,可建立关于a1和d的方程求出a1和d的值,从而求出通项
,可建立关于a1和d的方程求出a1和d的值,从而求出通项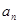 .
.
(2)再(1)的基础上可求出 ,再利用等比数列的定义可判断出
,再利用等比数列的定义可判断出 为等比数列;
为等比数列;
(3)由于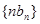 的通项为
的通项为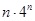 显然要采用错位相减的方法求和。
显然要采用错位相减的方法求和。
(1)设数列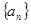 首项为
首项为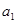 ,公差为
,公差为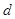
依题意得 ,………2分
,………2分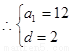 ………………3分
………………3分
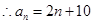 ……………4分
……………4分
(2)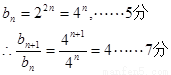
 是以
是以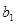 =4为首项,4为公比的等比数列。………………………8分
=4为首项,4为公比的等比数列。………………………8分
(3)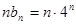 ……………………9分
……………………9分
 …………………11分
…………………11分
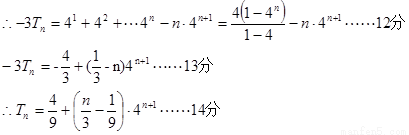
考点:等差数列的通项公式,等比数列的定义及通项公式及其前n项和公式,错位相减法求和。
点评:等差数列及等比数列的定义是判断数列是否是等差或等比数列的依据,并且要注意结合通项公式的特点判断选用何种方法求和,本题是一个等差数列与一个等比数列的积所以应采用错位相减法求和.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011年广东省揭阳市第一中学高二上学期期末检测数学文卷 题型:解答题
(本小题14分)在等比数列 中,
中, ,公比
,公比 ,且
,且 ,又
,又 与
与 的等比中项是2,
的等比中项是2,
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 .
.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二下学期第二次月考数学试卷(解析版) 题型:解答题
(本小题14分)在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛。
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为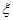 (
(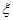 所有取值为0,1,2,3...,10)分别为
所有取值为0,1,2,3...,10)分别为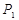 、
、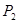 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
|
|
0 |
0 |
0 |
0 |
0.04 |
|
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
① 若1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
② ②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年广东省揭阳市高二上学期期末检测数学文卷 题型:解答题
(本小题14分)在等比数列 中,
中, ,公比
,公比 ,且
,且
 ,又
,又 与
与 的等比中项是2,
的等比中项是2,
(1)求数列 的通项公式;
的通项公式;
(2)设 ,数列
,数列 的前
的前 项和为
项和为 ,求
,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com