Question

9．设四边形ABCD为平行四边形，|$\overrightarrow{AB}$|=3，|$\overrightarrow{AD}$|=4，若点M、N满足$\overrightarrow{BM}$=3$\overrightarrow{MC}$，$\overrightarrow{DN}$=2$\overrightarrow{NC}$，则$\overrightarrow{AM}$•$\overrightarrow{NM}$=（　　）

• A． -1
• B． 0
• C． 1
• D． 2

Answer 1

分析 如图所示，$\overrightarrow{AM}$=$\overrightarrow{AB}+\overrightarrow{BM}$，$\overrightarrow{BM}=\frac{3}{4}\overrightarrow{BC}=\frac{3}{4}\overrightarrow{AD}$，$\overrightarrow{NM}$=$\overrightarrow{CM}-\overrightarrow{CN}$，$\overrightarrow{CM}$=-$\frac{1}{4}\overrightarrow{BC}$=-$\frac{1}{4}\overrightarrow{AD}$，$\overrightarrow{CN}$=-$\frac{1}{3}\overrightarrow{DC}$=-$\frac{1}{3}\overrightarrow{AB}$．代入展开即可得出．

解答 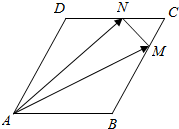解：如图所示，
$\overrightarrow{AM}$=$\overrightarrow{AB}+\overrightarrow{BM}$，$\overrightarrow{BM}=\frac{3}{4}\overrightarrow{BC}=\frac{3}{4}\overrightarrow{AD}$，$\overrightarrow{NM}$=$\overrightarrow{CM}-\overrightarrow{CN}$，$\overrightarrow{CM}$=-$\frac{1}{4}\overrightarrow{BC}$=-$\frac{1}{4}\overrightarrow{AD}$，$\overrightarrow{CN}$=-$\frac{1}{3}\overrightarrow{DC}$=-$\frac{1}{3}\overrightarrow{AB}$．
∴$\overrightarrow{AM}$•$\overrightarrow{NM}$=$（\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AD}）$•$（\frac{1}{3}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AD}）$=$\frac{1}{3}{\overrightarrow{AB}}^{2}$-$\frac{3}{16}{\overrightarrow{AD}}^{2}$=$\frac{1}{3}×{3}^{2}-\frac{3}{16}×{4}^{2}$=0．
故选：B．

点评 本题考查了向量共线定理、数量积运算性质，考查了推理能力与计算能力，属于中档题．