
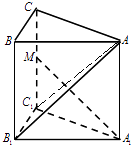
【题目】直三棱柱ABC﹣A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1= ![]() ,M是CC1的中点,则异面直线AB1与A1M所成角为 .
,M是CC1的中点,则异面直线AB1与A1M所成角为 .
【答案】![]()
【解析】解:连接AC1
∵∠ACB=90°,∠BAC=30°,BC=1,AA1= ![]() ,
,
∴A1C1= ![]() BC=
BC= ![]() ,
,
Rt△A1C1M中,tan∠A1MC1= ![]() ;
;
Rt△AA1C1中,tan∠AC1A1= ![]()
∴tan∠MA1C1=tan∠AC1A1 即∠AC1A1=∠A1MC1
可得矩形AA1C1C中,A1M⊥AC1
∵B1C1⊥A1C1 , B1C1⊥CC1且AC1∩CC1=C1
∴B1C1⊥平面AA1C1 ,
∵A1M面AA1C1 , ∴B1C1⊥A1M,
又AC1∩B1C1=C1 , ∴A1M⊥平面AB1C1
结合AB1平面AB1C1 , 得到AB1⊥A1M,
即异面直线AB1与A1M所成的角是 ![]() .
.
所以答案是: ![]() .
.
【考点精析】关于本题考查的异面直线及其所成的角,需要了解异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能得出正确答案.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)=Asin(ωx+![]() )+b (A>0,ω>0,|
)+b (A>0,ω>0,| ![]() |<
|<![]() )的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)的解析式为
)的模型波动(x为月份),已知3月份达到最高价9千元,7月份价格最低为5千元,根据以上条件可确定f(x)的解析式为
A. f(x)=2sin(![]() x-
x-![]() )+7 (1≤x≤12,x∈N+)
)+7 (1≤x≤12,x∈N+)
B. f(x)=9sin(![]() x-
x-![]() ) (1≤x≤12,x∈N+)
) (1≤x≤12,x∈N+)
C. f(x)=2![]() sin
sin![]() x+7 (1≤x≤12,x∈N+)
x+7 (1≤x≤12,x∈N+)
D. f(x)=2sin(![]() x+
x+![]() )+7 (1≤x≤2,x∈N+)
)+7 (1≤x≤2,x∈N+)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),┄,[80,90],并整理得到如下频率分布直方图:
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+4[sin(θ+ ![]() )]x﹣2,θ∈[0,2π]].
)]x﹣2,θ∈[0,2π]].
(1)若函数f(x)为偶函数,求tanθ的值;
(2)若f(x)在[﹣ ![]() ,1]上是单调函数,求θ的取值范围.
,1]上是单调函数,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设关于x的一元二次方程x2+2ax+b2=0.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com