
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)求出F(x)的导数,问题转化为8a≥(8x0-${{x}_{0}}^{2}$)max,x0∈(0,3],令g(x0)=8x0-${{x}_{0}}^{2}$=-${{(x}_{0}-4)}^{2}$+16,根据函数的单调性求出a的范围即可;
(3)求出lnx1x2-$\frac{2{(x}_{1}{+x}_{2})}{{{x}_{1}x}_{2}}$=$\frac{{{x}_{1}+x}_{2}}{{{x}_{2}-x}_{1}}$ln$\frac{{x}_{2}}{{x}_{1}}$,不妨设0<x1<x2,记t=$\frac{{x}_{2}}{{x}_{1}}$>1,令F(t)=lnt-$\frac{2(t-1)}{t+1}$,(t>1),根据函数的单调性求出ln$\sqrt{{{x}_{1}x}_{2}}$-$\frac{2}{\sqrt{{{x}_{1}x}_{2}}}$>1,解不等式即可.
解答 解:(1)f(x)=lnx-$\frac{3}{2}$x2-2x,定义域是(0,+∞),
f′(x)=$\frac{-(3x-1)(x+1)}{x}$,
令f′(x)>0,解得:0<x<$\frac{1}{3}$,令f′(x)<0,解得:x>$\frac{1}{3}$,
∴f(x)在(0,$\frac{1}{3}$)递增,在($\frac{1}{3}$,+∞)递减;
(2)F(x)=lnx+$\frac{a}{x}$,x∈(0,3],
则有k=F′(x0)=$\frac{{x}_{0}-a}{{{x}_{0}}^{2}}$≤$\frac{1}{8}$在x0(0,3]上恒成立,
∴8a≥(8x0-${{x}_{0}}^{2}$)max,x0∈(0,3],
令g(x0)=8x0-${{x}_{0}}^{2}$=-${{(x}_{0}-4)}^{2}$+16,
∴g(x0)在(0,3]递增,
∴g(x0)≤g(3)=24-9=15,
∴8a≥15,
解得:a≥$\frac{15}{8}$;
(3)H(x)=lnx-$\frac{1}{x}$,G(x)=mx,定义域是(0,+∞),
∴lnx1-$\frac{1}{{x}_{1}}$=mx1①,lnx2-$\frac{1}{{x}_{2}}$=mx2②,
①+②得:lnx1+lnx2-$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=m(x1+x2),
即lnx1x2-$\frac{{{x}_{1}+x}_{2}}{{{x}_{1}x}_{2}}$=m(x1+x2)③,
②-①得:lnx2-lnx1+$\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$=m(x2-x1),
即ln$\frac{{x}_{2}}{{x}_{1}}$+$\frac{{{x}_{2}-x}_{1}}{{{x}_{1}x}_{2}}$=m(x2-x1)④,
由③④得lnx1x2-$\frac{2{(x}_{1}{+x}_{2})}{{{x}_{1}x}_{2}}$=$\frac{{{x}_{1}+x}_{2}}{{{x}_{2}-x}_{1}}$ln$\frac{{x}_{2}}{{x}_{1}}$,
不妨设0<x1<x2,记t=$\frac{{x}_{2}}{{x}_{1}}$>1,
令F(t)=lnt-$\frac{2(t-1)}{t+1}$,(t>1),
∴F′(t)=$\frac{{(t-1)}^{2}}{t(t+1)}$>0,
∴F(t)在(1,+∞)递增,∴F(t)>F(1)=0,
∴lnt>$\frac{2(t-1)}{t+1}$,即ln$\frac{{x}_{2}}{{x}_{1}}$>$\frac{2{(x}_{2}{-x}_{1})}{{{x}_{1}+x}_{2}}$,
∴lnx1x2-$\frac{2{(x}_{1}{+x}_{2})}{{{x}_{1}x}_{2}}$=$\frac{{{x}_{1}+x}_{2}}{{{x}_{2}-x}_{1}}$ln$\frac{{x}_{2}}{{x}_{1}}$>2,
∴lnx1x2-$\frac{2{(x}_{1}{+x}_{2})}{{{x}_{1}x}_{2}}$<lnx1x2-$\frac{4\sqrt{{{x}_{1}x}_{2}}}{{{x}_{1}x}_{2}}$=lnx1x2-$\frac{4}{\sqrt{{{x}_{1}x}_{2}}}$=2ln$\sqrt{{{x}_{1}x}_{2}}$-$\frac{4}{\sqrt{{{x}_{1}x}_{2}}}$,
∴2ln$\sqrt{{{x}_{1}x}_{2}}$-$\frac{4}{\sqrt{{{x}_{1}x}_{2}}}$>2,即ln$\sqrt{{{x}_{1}x}_{2}}$-$\frac{2}{\sqrt{{{x}_{1}x}_{2}}}$>1,
令ω(x)=lnx-$\frac{2}{x}$,
∴ω′(x)=$\frac{1}{x}$+$\frac{2}{{x}^{2}}$>0,
∴ω(x)在(0,+∞)递增,
又ln($\sqrt{2}$e)-$\frac{2}{\sqrt{2}e}$=$\frac{1}{2}$ln2+1-$\frac{\sqrt{2}}{e}$<1,
∴ln$\sqrt{{{x}_{1}x}_{2}}$-$\frac{2}{\sqrt{{{x}_{1}x}_{2}}}$>1>ln($\sqrt{2}$e)-$\frac{2}{\sqrt{2}e}$,
即ω($\sqrt{{{x}_{1}x}_{2}}$)>ω($\sqrt{2}$e),
∴$\sqrt{{{x}_{1}x}_{2}}$>$\sqrt{2}$e,
∴x1x2>2e2.
点评 本题考查函数的单调性问题,考查了利用导数求函数的最值,体现了数学转化思想方法和函数构造法,本题综合考查了学生的逻辑思维能力和灵活应变能力,难度较大.


科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
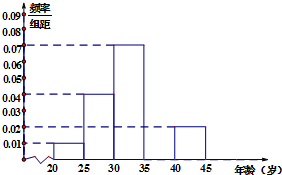 随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.
随着科技的发展,手机已经成为人们不可或缺的交流工具,除传统的打电话外,手机的功能越来越强大,人们可以玩游戏,看小说,观电影,逛商城等,真是“一机在手,天下我有”,所以,有人把喜欢玩手机的人冠上了名号“低头族”,低头族已经严重影响了人们的生活,一媒体为调查市民对低头族的认识,从某社区的500名市民中,随机抽取100名市民,按年龄情况进行统计的频率分布表和频率分布直方图.| 分组(单位:岁) | 频数 | 频率 |
| [20,25) | 5 | 0.05 |
| [25,30) | 20 | 0.20 |
| [30,35) | ① | 0.350 |
| [35,40) | 30 | ② |
| [40,45] | 10 | 0.10 |
| 合计 | 100 | 1.000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
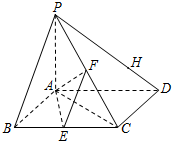 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com