
设点A为半径是1的圆O上一定点,在圆周上等可能地任取一点B.
(1)求弦AB的长超过圆内接正三角形边长的概率;
(2)求弦AB的长超过圆半径的概率.

(1)弦AB的长超过圆内接正三角形边长的概率为 .(2)弦AB的长超过圆的半径的概率是
.(2)弦AB的长超过圆的半径的概率是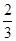 .
.
【解析】(1) 设“弦AB的长超过圆内接正三角形边长”为事件M,以点A为一顶点,在圆中作一圆内接正三角形ACD,则要满足题意点B只能落在劣弧CD上,又圆内接正三角形ACD恰好将圆周3等分,這樣可得出劣弧CD的長占整個圓周長的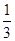 .
.
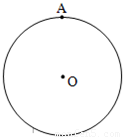
(2) 以圆的半径OA为边长作出两正三角形AOC和AOD,如图所示,
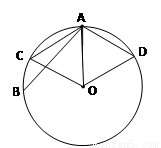
则AC=AD=圆的半径OA,所以满足题意的点B只能落在优弧CD上,然后求出对应的角 ,从而可求出优弧CD的对应的圆心角,进而得到优弧CD的长,其概率等于
,从而可求出优弧CD的对应的圆心角,进而得到优弧CD的长,其概率等于 .
.
解:(1)设“弦AB的长超过圆内接正三角形边长”为事件M,以点A为一顶点,在圆中作一圆内接正三角形ACD,如右图所示,
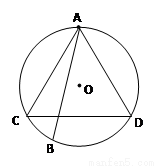
则要满足题意点B只能落在劣弧CD上,又圆内接正三角形ACD恰好将圆周3等分,故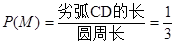 . ……6分
. ……6分
答:弦AB的长超过圆内接正三角形边长的概率为 .
.
(2)设“弦AB的长超过圆的半径”为事件N,
以圆的半径OA为边长作出两正三角形AOC和AOD,如图所示,

则AC=AD=圆的半径OA,所以满足题意的点B只能落在优弧CD上,
又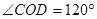 ,故劣弧CD的长为
,故劣弧CD的长为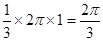 ,即优弧CD的长为
,即优弧CD的长为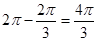
所以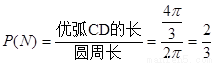 .
.
答:弦AB的长超过圆的半径的概率是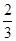 . ……12分
. ……12分


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设点A为半径是1的圆O上一定点,在圆周上等可能地任取一点B.
设点A为半径是1的圆O上一定点,在圆周上等可能地任取一点B.查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省三明一中高二(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com