
| A. | 2 | B. | -1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
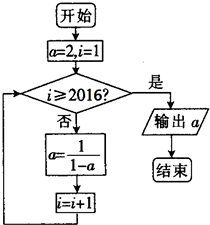
分析 执行程序框图,写出每次循环得到的i,a的值,当i=2015时不满足条件i≥2016,a=$\frac{1}{2}$,当i=2016时满足条件i≥2016,输出a的值为$\frac{1}{2}$.
解答 解:模拟执行程序框图,有
a=2,i=1
不满足条件i≥2016,执行循环体,a=-1,i=2
不满足条件i≥2016,执行循环体,a=$\frac{1}{2}$,i=3
不满足条件i≥2016,执行循环体,a=2,i=4
不满足条件i≥2016,执行循环体,a=-1,i=5
不满足条件i≥2016,执行循环体,a=$\frac{1}{2}$,
…
由此分析可得结论,程序框图的作用是计算输出a的值,a的取值以3为周期,
因为2015=3×671+2,故有
i=2015,不满足条件i≥2016,a=$\frac{1}{2}$,i=2016,
此时,满足条件i≥2016,输出a的值为$\frac{1}{2}$.
故选:C.
点评 本题主要考察了程序框图和算法的应用,模拟执行程序,分析程序算法的功能是解题的关键,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 3,7 | B. | 3,5 | C. | 5,7 | D. | 2$\sqrt{2}$,5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -$\frac{1}{4}$ | C. | 5 | D. | -$\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
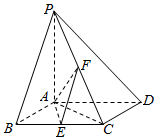 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,BC边上的中线AD长为3,且cosB=$\frac{{\sqrt{10}}}{8}$,cos∠ADC=-$\frac{1}{4}$.
如图,在△ABC中,BC边上的中线AD长为3,且cosB=$\frac{{\sqrt{10}}}{8}$,cos∠ADC=-$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
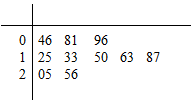 某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:
某市对居民在某一时段用电量(单位:度)进行调查后,为对数据进行分析统计,按照数据大、小将数据分成A、B、C三组,如表所示:| 分组 | A | B | C |
| 用电量 | (0,80] | (80,250] | (250,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10或-$\frac{7}{2}$ | B. | 4或-$\frac{5}{4}$ | C. | 4或-$\frac{7}{2}$ | D. | 10或-$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{2}$,1] | B. | (-∞,$\frac{1}{2}$]∪[1,+∞) | C. | [-$\frac{1}{2}$,1] | D. | (-∞,-$\frac{1}{2}$)∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∪N=U | B. | M∩N=N | C. | M∩(∁UN)=∅ | D. | M⊆∁UN |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com