
已知在数列![]() 中,
中,![]() ,
,![]() (
(![]() ÎR,
ÎR,![]() ÎR 且
ÎR 且![]() ¹0,
¹0,![]() N
N![]() ).
).
(1)若数列![]() 是等比数列,求
是等比数列,求![]() 与
与![]() 满足的条件;
满足的条件;
(2)当![]() ,
,![]() 时,一个质点在平面直角坐标系内运动,从坐标原点出发,第1次向右运动,第2次向上运动,第3次向左运动,第4次向下运动,以后依次按向右、向上、向左、向下的方向交替地运动,设第
时,一个质点在平面直角坐标系内运动,从坐标原点出发,第1次向右运动,第2次向上运动,第3次向左运动,第4次向下运动,以后依次按向右、向上、向左、向下的方向交替地运动,设第![]() 次运动的位移是
次运动的位移是![]() ,第
,第![]() 次运动后,质点到达点
次运动后,质点到达点![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
科目:高中数学 来源: 题型:
已知在数列![]() 中,
中,![]() (
(![]() ).
).
(I)若q =2,d = -1,,求a3,a4,并猜测a2006;
(II)若![]() 是等比数列,且
是等比数列,且![]() 是等差数列,求q, d满足的条件.
是等差数列,求q, d满足的条件.
查看答案和解析>>
科目:高中数学 来源:2012届黑龙江省双鸭山一中高三上学期期中考试理科数学 题型:解答题
(本小题满分12分)
已知在数列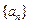 中,
中,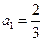
 ,
,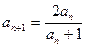 ,
,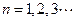
(1) 证明:数列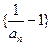 是
是 等比数列; (2)求数列
等比数列; (2)求数列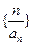 的前n项和。
的前n项和。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省温州市高三第一次月考文科数学试卷(解析版) 题型:解答题
(本题满分14分) 已知在数列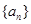 中,
中,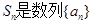 的前n项和,
的前n项和,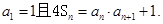
(1)求数列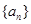 的通项公式;
的通项公式;
(2)令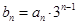 ,数列
,数列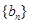 的前n项和为
的前n项和为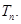 求
求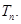
查看答案和解析>>
科目:高中数学 来源:2011-2012学年黑龙江省高三上学期期中考试理科数学 题型:解答题
(本小题满分12分)
已知在数列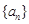 中,
中,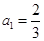 ,
,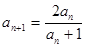 ,
,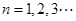
(1) 证明:数列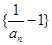 是等比数列; (2)求数列
是等比数列; (2)求数列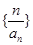 的前n项和。
的前n项和。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省赣州市高三第四次月考理科数学 题型:解答题
14分)已知在数列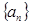 中,
中,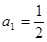 ,
,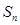 是其前
是其前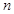 项和,且
项和,且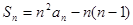 .
.
(1)证明:数列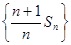 是等差数列;
是等差数列;
(2)令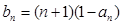 ,记数列
,记数列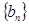 的前
的前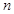 项和为
项和为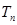 .
.
①;求证:当 时,
时,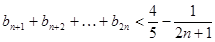
②: 求证:当 时,
时,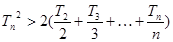
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com