解:(Ⅰ)由条件可知,点P到两定点F
1(1,0),F
2(-1,0)的距离之和为定值

,
所以点P的轨迹是以F
1(1,0),F
2(-1,0)为焦点的椭圆.…(2分)
又

,c=1,所以b=1,
故所求方程为

.…(4分)
(Ⅱ)设A(x
1,y
1),B(x
2,y
2),C(x
3,y
3).
由
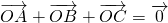
,得x
1+x
2+x
3=0,y
1+y
2+y
3=0.…(5分)
(ⅰ)可设直线AB的方程为y=kx+n(k≠0),
代入x
2+2y
2=2并整理得,(1+2k
2)x
2+4knx+2n
2-2=0,
依题意,△>0,则
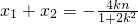
,
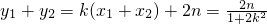
,
从而可得点C的坐标为
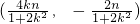
,
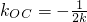
.
因为
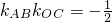
,所以直线AB与OC的斜率之积为定值.…(8分)
(ⅱ)若AB⊥x轴时,

,由
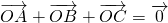
,
得点C(2,0),所以点C不在椭圆Γ上,不合题意.
因此直线AB的斜率存在.…(9分)
由(ⅰ)可知,当直线AB过点F
1时,有n=k,点C的坐标为
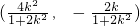
.
代入x
2+2y
2=2得,
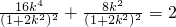
,即4k
2=1+2k
2,
所以
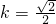
. …(11分)
(1)当
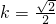
时,由(ⅰ)知,
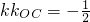
,从而
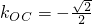
.
故AB、OC及x轴所围成三角形为等腰三角形,其底边长为1,且底边上的高
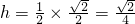
,所求等腰三角形的面积
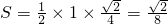
.
(2)当
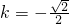
时,又由(ⅰ)知,
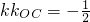
,从而
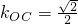
,
同理可求直线AB、OC与x轴所围成的三角形的面积为
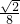
.
综合(1)(2),直线AB、OC与x轴所围成的三角形的面积为
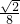
.…(13分)
分析:(Ⅰ)根据椭圆的定义,可知点P的轨迹是以F
1(1,0),F
2(-1,0)为焦点的椭圆,进而可得曲线Γ的方程;
(Ⅱ)将
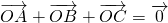
转化为坐标之间的关系.(ⅰ)设直线AB的方程代入椭圆方程并整理,利用韦达定理,确定点C的坐标,利用斜率公式可得直线AB与OC的斜率之积为定值;(ⅱ)先判断直线AB的斜率存在,确定点C的坐标代入椭圆方程,可求k的值,进而分类求出直线AB、OC与x轴所围成的三角形的面积.
点评:本小题考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想等.

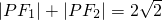 ,记点P的轨迹为曲线Γ.
,记点P的轨迹为曲线Γ.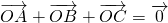 .
. ,
, ,c=1,所以b=1,
,c=1,所以b=1, .…(4分)
.…(4分)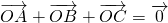 ,得x1+x2+x3=0,y1+y2+y3=0.…(5分)
,得x1+x2+x3=0,y1+y2+y3=0.…(5分)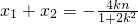 ,
,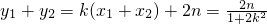 ,
,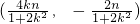 ,
,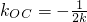 .
.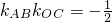 ,所以直线AB与OC的斜率之积为定值.…(8分)
,所以直线AB与OC的斜率之积为定值.…(8分) ,由
,由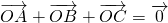 ,
,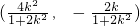 .
.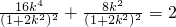 ,即4k2=1+2k2,
,即4k2=1+2k2,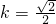 . …(11分)
. …(11分)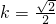 时,由(ⅰ)知,
时,由(ⅰ)知,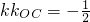 ,从而
,从而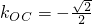 .
.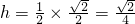 ,所求等腰三角形的面积
,所求等腰三角形的面积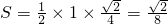 .
.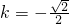 时,又由(ⅰ)知,
时,又由(ⅰ)知,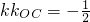 ,从而
,从而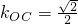 ,
,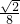 .
.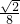 .…(13分)
.…(13分)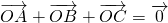 转化为坐标之间的关系.(ⅰ)设直线AB的方程代入椭圆方程并整理,利用韦达定理,确定点C的坐标,利用斜率公式可得直线AB与OC的斜率之积为定值;(ⅱ)先判断直线AB的斜率存在,确定点C的坐标代入椭圆方程,可求k的值,进而分类求出直线AB、OC与x轴所围成的三角形的面积.
转化为坐标之间的关系.(ⅰ)设直线AB的方程代入椭圆方程并整理,利用韦达定理,确定点C的坐标,利用斜率公式可得直线AB与OC的斜率之积为定值;(ⅱ)先判断直线AB的斜率存在,确定点C的坐标代入椭圆方程,可求k的值,进而分类求出直线AB、OC与x轴所围成的三角形的面积.
