
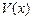 。
。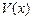 的解析式,并求出函数的定义域;
的解析式,并求出函数的定义域;
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:不详 题型:单选题
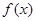 满足
满足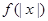 =|
=|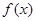 |,则称
|,则称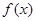 为对等函数,
为对等函数,| A.0; | B.1; | C.2; | D.3. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
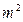 ,计划1998年底人均住房面积达10
,计划1998年底人均住房面积达10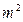 。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万
。如果该市每年人口平均增长率控制在1%,要实现上述计划,这个城市每年平均至少要新增住房面积多少万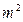 (结果以万
(结果以万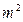 为单位,保留两位小数)。
为单位,保留两位小数)。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
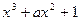 的图象上一点B(1,b)的切线的斜率为-3.
的图象上一点B(1,b)的切线的斜率为-3.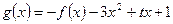 .是否存在一个实数t,使得当
.是否存在一个实数t,使得当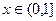 时,g(x)有最大值1?
时,g(x)有最大值1?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com