
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1 , BC1 , AC上的正投影都为三角形时,将它们的面积分别记为S1 , S2 , S3 . 
(i)当BP= ![]() 时,S1S2(填“>”或“=”或“<”);
时,S1S2(填“>”或“=”或“<”);
(ii) S1+S2+S3的最大值为 .
科目:高中数学 来源: 题型:
【题目】对函数f(x),如果存在x0≠0使得f(x0)=﹣f(﹣x0),则称(x0 , f(x0))与(﹣x0 , f(﹣x0))为函数图象的一组奇对称点.若f(x)=ex﹣a(e为自然数的底数)存在奇对称点,则实数a的取值范围是( )
A.(﹣∞,1)
B.(1,+∞)
C.(e,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为4的正三角形ABC中,D,F分别为AB,AC的中点,E为AD的中点.将△BCD与△AEF分别沿CD,EF同侧折起,使得二面角A﹣EF﹣D与二面角B﹣CD﹣E的大小都等于90°,得到如图2所示的多面体. 
(1)在多面体中,求证:A,B,D,E四点共同面;
(2)求多面体的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0,10) | 2 |
[10,20) | 3 |
[20,30) | 5 |
[30,40) | 15 |
[40,50) | 40 |
[50,60] | 35 |

(Ⅰ)在抽样的100人中,求对A餐厅评分低于30的人数;
(Ⅱ)从对B餐厅评分在[0,20)范围内的人中随机选出2人,求2人中恰有1人评分在[0,10)范围内的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调研学生在A,B两家餐厅用餐的满意度,从在A,B两家餐厅都用过餐的学生中随机抽取了100人,每人分别对这两家餐厅进行评分,满分均为60分.整理评分数据,将分数以10为组距分成6组:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60],得到A餐厅分数的频率分布直方图,和B餐厅分数的频数分布表:
B餐厅分数频数分布表 | |
分数区间 | 频数 |
[0,10) | 2 |
[10,20) | 3 |
[20,30) | 5 |
[30,40) | 15 |
[40,50) | 40 |
[50,60] | 35 |
定义学生对餐厅评价的“满意度指数”如下:
分数 | [0,30) | [30,50) | [50,60] |
满意度指数 | 0 | 1 | 2 |

(Ⅰ)在抽样的100人中,求对A餐厅评价“满意度指数”为0的人数;
(Ⅱ)从该校在A,B两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对A餐厅评价的“满意度指数”比对B餐厅评价的“满意度指数”高的概率;
(Ⅲ)如果从A,B两家餐厅中选择一家用餐,你会选择哪一家?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() +c(e=2.71828…是自然对数的底数,c∈R).
+c(e=2.71828…是自然对数的底数,c∈R).
(Ⅰ)求f(x)的单调区间、最大值;
(Ⅱ)讨论关于x的方程|lnx|=f(x)根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B是海面上两个固定观测站,现位于B点南偏东45°且相距 ![]() 海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距
海里的D处有一艘轮船发出求救信号.此时在A处观测到D位于其北偏东30°处,位于A北偏西30°且与A相距 ![]() 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高一、高二年级各有8个班,学校调查了春学期各班的文学名著阅读量(单位:本),并根据调查结果,得到如下所示的茎叶图: 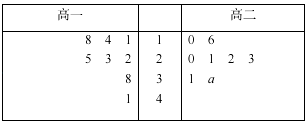
为鼓励学生阅读,在高一、高二两个两个年级中,学校将阅读量高于本年级阅读量平均数的班级命名为该年级的“书香班级”.
(1)当a=4时,记高一年级“书香班级”数为m,高二年级的“书香班级”数为n,比较m,n的大小关系;
(2)在高一年级8个班级中,任意选取两个,求这两个班级均是“书香班级”的概率;
(3)若高二年级的“书香班级”数多于高一年级的“书香班级”数,求a的值(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com