解:(1)cosB=cos2C=2cos
2c-1=

∴sinB=
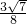
∵cosC=

得sinC=

∴cosA=-cos(B+C)=-(cosBcosC-sinBsinC)=

(2)由
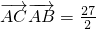
得bc•cosA=

即bc=24
又
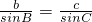
,即
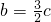
b=6,c=4
∴a
2=b
2+c
2-2bccosA=36+16-27=25∴a=5,即BC=5
分析:(1)根据cosB=cos2C求出cosB的值,进而得出sinB的值,然后根据cosA=cos[π-(B+C)]=-cos(B+C),由余弦的两角和与差公式得出结果即可;
(2)首先根据向量积求出bc的值,然后根据正弦定理求出b和c的值,再由余弦定理得出结果.
点评:本题考查了正弦定理、余弦定理、同角三角函数的基本关系以及余弦的两角和与差公式,(1)问中要注意cosA=cos[π-(B+C)]的运用,属于中档题.

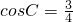 ,
,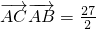 (1)求cosA的值.(2)求边BC的长.
(1)求cosA的值.(2)求边BC的长.
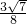
 得sinC=
得sinC=

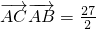 得bc•cosA=
得bc•cosA= 即bc=24
即bc=24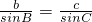 ,即
,即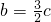 b=6,c=4
b=6,c=4
