
 满足
满足 +
+ =4n-3(n∈
=4n-3(n∈ ).
). 是等差数列,求
是等差数列,求 的值;
的值; =2时,求数列
=2时,求数列 的前n项和
的前n项和 ;
; ,都有
,都有 ≥5成立,求
≥5成立,求 的取值范围.
的取值范围. ;⑵
;⑵ =
=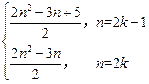 (k∈Z);⑶
(k∈Z);⑶ ,
, ,
, .
. 是等差数列,则
是等差数列,则 =
= +(n-1)d,
+(n-1)d, =
= +nd.
+nd. +
+ =4n-3,得(
=4n-3,得( +nd)+[
+nd)+[ +(n-1)d]=4n-3,即2d=4,
+(n-1)d]=4n-3,即2d=4, -d=-3,解得d=2,
-d=-3,解得d=2, =
= .
. +
+ =4n-3(n∈
=4n-3(n∈ ),得
),得 +
+ =4n+1(n∈
=4n+1(n∈ ).
). -
- =4.
=4.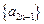 是首项为
是首项为 ,公差为4的等差数列.
,公差为4的等差数列.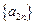 是首项为
是首项为 ,公差为4的等差数列.
,公差为4的等差数列. +
+ =1,
=1, =2,得
=2,得 =-1.
=-1. =
= (k∈Z).①当n为奇数时,
(k∈Z).①当n为奇数时, =2n,
=2n, =2n-3.
=2n-3. =
= +
+ +
+ +…+
+…+ =(
=( +
+ )+(
)+( +
+ )+…+(
)+…+( +
+ )+
)+
 +2n=
+2n= .
. =
= +
+ +
+ +…+
+…+ =(
=( +
+ )+(
)+( +
+ )+…+(
)+…+( +
+ )==1+9+…+(4n-7) =
)==1+9+…+(4n-7) = .
. =
=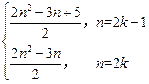 (k∈Z).
(k∈Z). =
= (k∈Z).
(k∈Z). =2n-2+
=2n-2+ ,
, =2n-1-
=2n-1- .
. ≥5,得
≥5,得 -
- ≥
≥ +16n-10.
+16n-10. =
= +16n-10=
+16n-10= +6.
+6. =2,所以
=2,所以 -
- ≥2.
≥2. ≥2或
≥2或 ≤-1.
≤-1. =2n-3-
=2n-3- ,
, =2n+
=2n+ .
. ≥5,得
≥5,得 +
+ ≥
≥ +16n-12.
+16n-12. =
= +16n-12=
+16n-12= +4.
+4. =4,所以
=4,所以 +
+ ≥4.
≥4. ≥1或
≥1或 ≤-4.
≤-4. 的取值范围是
的取值范围是 ,
, ,
, .
.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源:不详 题型:解答题
 )个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
)个圆盘依其半径大小,大的在下,小的在上套在A柱上,现要将套在A柱上的盘换到C柱上,要求每次只能搬动一个,而且任何时候不允许将大盘套在小盘上面,假定有三根柱子A、B、C可供使用.
 ,求和
,求和 (
( );(其中
);(其中 表示所有的积
表示所有的积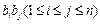 的和)
的和)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 14分)已知数列
14分)已知数列 是以
是以 d为公差的等差数列,数列
d为公差的等差数列,数列 是以q为公比的
是以q为公比的 的前n项和为
的前n项和为 且
且 ,求整数q的值;
,求整数q的值; 中最否存在一项
中最否存在一项 ,使得
,使得 恰好可以表示为该数列
恰好可以表示为该数列 项的和?请说明理由;
项的和?请说明理由; ,求证:数列
,求证:数列
 中的项。
中的项。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com