
【题目】已知椭圆 ![]() =1(a>b>0)经过点(
=1(a>b>0)经过点( ![]() ,﹣
,﹣ ![]() ),且椭圆的离心率e=
),且椭圆的离心率e= ![]() .
.
(1)求椭圆的方程;
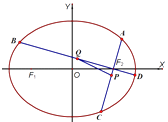
(2)过椭圆的右焦点F作两条互相垂直的直线,分别交椭圆于点A,C及B,D,设线段AC,BD的中点分别为P,Q.求证:直线PQ恒过一个定点.
【答案】
(1)解:由 ![]() ,得
,得 ![]() ,
,
即a2=4c2=4(a2﹣b2),即3a2=4b2. …
由椭圆过点 ![]() 知,
知, ![]() . …
. …
联立(1)、(2)式解得a2=4,b2=3. …
故椭圆的方程是 ![]() .…
.…
(2)证明:直线PQ恒过一个定点 ![]() .…
.…
椭圆的右焦点为F(1,0),分两种情况.
1°当直线AC的斜率不存在时,
AC:x=1,则 BD:y=0.由椭圆的通径得P(1,0),
又Q(0,0),此时直线PQ恒过一个定点 ![]() .…
.…
2°当直线AC的斜率存在时,设AC:y=k(x﹣1)(k≠0),
则 BD: ![]() .
.
又设点A(x1,y1),C(x2,y2).
联立方程组 ![]() ,
,
消去y并化简得(4k2+3)x2﹣8k2x+4k2﹣12=0,…
所以 ![]() .
. ![]() .
. ![]() .…
.…
由题知,直线BD的斜率为﹣ ![]() ,
,
同理可得点 ![]() .…
.…
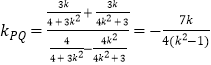 .
.
![]() ,…
,…
即4yk2+(7x﹣4)k﹣4y=0.
令4y=0,7x﹣4=0,﹣4y=0,解得 ![]() .
.
故直线PQ恒过一个定点 ![]() ;…
;…
综上可知,直线PQ恒过一个定点 ![]() .…
.…
【解析】(1)由离心率可得a与c的关系,过点![]() 可得a与b的关系,再根据
可得a与b的关系,再根据![]() ,即可得出椭圆方程;(2)当斜率不存在时,得出此时过定点
,即可得出椭圆方程;(2)当斜率不存在时,得出此时过定点![]() ,当斜率存在时,根据点斜式设出两相互垂直的直线方程,代入椭圆方程,由韦达定理可得P、Q的坐标,再得出PQ所在直线方程,经检验PQ过点
,当斜率存在时,根据点斜式设出两相互垂直的直线方程,代入椭圆方程,由韦达定理可得P、Q的坐标,再得出PQ所在直线方程,经检验PQ过点![]() 。
。


科目:高中数学 来源: 题型:
【题目】各项为正的数列{an}满足 ![]() ,
,
(1)当λ=an+1时,求证:数列{an}是等比数列,并求其公比;
(2)当λ=2时,令 ![]() ,记数列{bn}的前n项和为Sn , 数列{bn}的前n项之积为Tn , 求证:对任意正整数n,2n+1Tn+Sn为定值.
,记数列{bn}的前n项和为Sn , 数列{bn}的前n项之积为Tn , 求证:对任意正整数n,2n+1Tn+Sn为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() (a>b>0)的右准线的方程为x=
(a>b>0)的右准线的方程为x= ![]() ,左、右两个焦点分别为F1(
,左、右两个焦点分别为F1( ![]() ),F2(
),F2( ![]() ).
).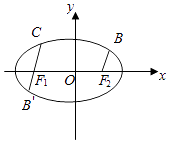
(1)求椭圆E的方程;
(2)过F1 , F2两点分别作两条平行直线F1C和F2B交椭圆E于C,B两点(C,B均在x轴上方),且F1C+F2B等于椭圆E的短轴的长,求直线F1C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[0,1]上的函数满足:①f(0)=f(1)=0,②对于所有x,y∈[0,1]且x≠y有|f(x)﹣f(y)|< ![]() |x﹣y|.若当所有的x,y∈[0,1]时,|f(x)﹣f(y)|<k,则k的最小值为 .
|x﹣y|.若当所有的x,y∈[0,1]时,|f(x)﹣f(y)|<k,则k的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣1(e为自然对数的底数).
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当a>0时,若f(x)≥0对任意的x∈R恒成立,求实数a的值;
(Ⅲ)求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“全面二孩”政策推行,我市将迎来生育高峰.今年新春伊始,泉城各医院产科就已经是一片忙碌至今热度不减.卫生部门进行调查统计期间发现各医院的新生儿中,不少都是“二孩”;在市第一医院,共有40个猴宝宝降生,其中10个是“二孩”宝宝;
(Ⅰ)从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询,
①在市第一医院出生的一孩宝宝中抽取多少个?
②若从7个宝宝中抽取两个宝宝进行体检,求这两个宝宝恰出生不同医院且均属“二孩”的概率;
(II)根据以上数据,能否有85%的把握认为一孩或二孩宝宝的出生与医院有关?
P(k≥k市) | 0.40 | 0.25 | 0.15 | 0.10 |
k市 | 0.708 | 1.323 | 2.072 | 2.706 |
K2= ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com