Question

【题目】直三棱柱ABC﹣A1B1C1 中，AA1=AB=AC=1，E，F分别是CC1、BC 的中点，AE⊥ A1B1 ， D为棱A1B1上的点．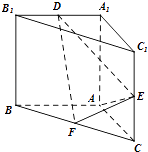

（1）证明：DF⊥AE；
（2）是否存在一点D，使得平面DEF与平面ABC所成锐二面角的余弦值为 ？若存在，说明点D的位置，若不存在，说明理由．

Answer 1

【答案】
（1）证明：∵AE⊥A1B1，A1B1∥AB，∴AE⊥AB，

又∵AA1⊥AB，AA1⊥∩AE=A，∴AB⊥面A1ACC1，

又∵AC面A1ACC1，∴AB⊥AC，

以A为原点建立如图所示的空间直角坐标系A﹣xyz，

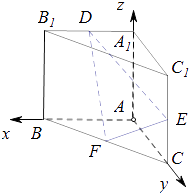
则有A（0，0，0），E（0，1， ），F（ ， ，0），A1（0，0，1），B1（1，0，1），

设D（x，y，z）， 且λ∈[0，1]，即（x，y，z﹣1）=λ（1，0，0），

则 D（λ，0，1），所以 =（ ， ，﹣1），

∵ =（0，1， ），∴ = =0，所以DF⊥AE

（2）结论：存在一点D，使得平面DEF与平面ABC所成锐二面角的余弦值为 ．

理由如下：

设面DEF的法向量为 =（x，y，z），则 ，

∵ =（ ， ， ）， =（ ，﹣1），

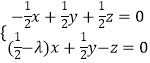∴ ，即 ，

令z=2（1﹣λ），则 =（3，1+2λ，2（1﹣λ））．

由题可知面ABC的法向量 =（0，0，1），

∵平面DEF与平面ABC所成锐二面角的余弦值为 ，

∴|cos＜ ， ＞|= = ，即 = ，

解得 或 （舍），所以当D为A1B1中点时满足要求．

【解析】（1）先证明AB⊥AC，然后以A为原点建立空间直角坐标系A﹣xyz，则能写出各点坐标，由 与 共线可得D（λ，0，1），所以 =0，即DF⊥AE；（2）通过计算，面DEF的法向量为 可写成 =（3，1+2λ，2（1﹣λ）），又面ABC的法向量 =（0，0，1），令|cos＜ ， ＞|= ，解出λ的值即可．
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识，掌握垂直于同一个平面的两条直线平行．