
【题目】已知命题p:“1≤x≤5是x2﹣(a+1)x+a≤0的充分不必要条件”,命题q:“满足AC=6,BC=a,∠CAB=30°的△ABC有两个”.若¬p∧q是真命题,求实数a的取值范围.
【答案】解:对于命题p:“1≤x≤5是x2﹣(a+1)x+a≤0的充分不必要条件”, ∴1≤x≤5是1≤x≤a的真子集
∴a>5
对于命题q:“满足AC=6,BC=a,∠CAB=30°的△ABC有两个”.
∴3<a<6
∵若¬p∧q是真命题
∴p假q真则 ![]() ,
,
综上,实数a的取值范围:3<a≤5
【解析】本题的关键是给出命题p:“1≤x≤5是x2﹣(a+1)x+a≤0的充分不必要条件”,命题q:“满足AC=6,BC=a,∠CAB=30°的△ABC有两个”为真时a的取值范围,在利用p假q真给出a的取值范围
【考点精析】认真审题,首先需要了解复合命题的真假(“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真).


科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,满足a1=3,a4=12,数列{bn}满足b1=4,b4=20,且{bn﹣an}为等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点A,B分别是椭圆 ![]() 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: ![]() 且PA⊥PF.
且PA⊥PF. 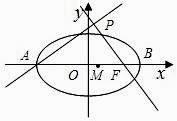
(1)求直线AP的方程;
(2)设点M是椭圆长轴AB上一点,点M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列命题:( )
①向量 ![]() ,
, ![]() 不共线,则向量
不共线,则向量 ![]() 与向量
与向量 ![]() 一定不共线
一定不共线
②对任意向量 ![]() ,
, ![]() ,则
,则 ![]() 恒成立
恒成立
③在同一平面内,对两两均不共线的向量 ![]() ,
, ![]() ,
, ![]() ,若给定单位向量
,若给定单位向量 ![]() 和正数
和正数 ![]() ,总存在单位向量
,总存在单位向量 ![]() 和实数
和实数 ![]() ,使得
,使得 ![]()
则正确的序号为( )
A.①②③
B.①③
C.②③
D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1 中,AA1=AB=AC=1,E,F分别是CC1、BC 的中点,AE⊥ A1B1 , D为棱A1B1上的点.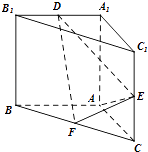
(1)证明:DF⊥AE;
(2)是否存在一点D,使得平面DEF与平面ABC所成锐二面角的余弦值为 ![]() ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2cos(x﹣ ![]() )的图象上所有的点的横坐标缩短到原来的
)的图象上所有的点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
倍(纵坐标不变),得到函数y=g(x)的图象,则函数y=g(x)的图象( )
A.关于点(﹣ ![]() ,0)对称
,0)对称
B.关于点( ![]() ,0)对称
,0)对称
C.关于直线x=﹣ ![]() 对称
对称
D.关于直线x= ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABP7P5的边长为2,P1 , P4 , P6 , P2是四边的中点,AB是正方形的其中一条边,P1P6与P2P4相交于点P3 , 则 ![]()
![]() (i=1,2,…,7)的不同值的个数为( )
(i=1,2,…,7)的不同值的个数为( ) 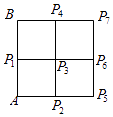
A.7
B.5
C.3
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量 ![]() =(c+a,b),
=(c+a,b), ![]() =(c﹣a,b﹣c),且
=(c﹣a,b﹣c),且 ![]() ⊥
⊥ ![]() .
.
(1)求角A的大小;
(2)若a=3,求△ABC周长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com