若数列{an}满足:a1=m1,a2=m2,an+2=pan+1+qan(p,q是常数),则称数列{an}为二阶线性递推数列,且定义方程x2=px+q为数列{an}的特征方程,方程的根称为特征根; 数列{an}的通项公式an均可用特征根求得:
①若方程x2=px+q有两相异实根α,β,则数列通项可以写成an=c1αn+c2βn,(其中c1,c2是待定常数);
②若方程x2=px+q有两相同实根α,则数列通项可以写成an=(c1+nc2)αn,(其中c1,c2是待定常数);
再利用a1=m1,a2=m2,可求得c1,c2,进而求得an.根据上述结论求下列问题:
(1)当a1=5,a2=13,an+2=5an+1-6an(n∈N*)时,求数列{an}的通项公式;
(2)当a1=1,a2=11,an+2=2an+1+3an+4(n∈N*)时,求数列{an}的通项公式;
(3)当a1=1,a2=1,an+2=an+1+an(n∈N*)时,记Sn=a1Cn1+a2Cn2+…+anCnn,若Sn能被数8整除,求所有满足条件的正整数n的取值集合.
解:(1)由a
n+2=5a
n+1-6a
n可知特征方程为:x
2-5x+6=0,x
1=2,x
2=3…(3分)
所以 设 a
n=c
1•2
n+c
2•3
n,由

得到c
1=c
2=1,
所以 a
n=2
n+3
n; …(6分)
(2)由a
n+2=2a
n+1+3a
n+4可以得到(a
n+2+1)=2(a
n+1+1)+3(a
n+1)
设b
n=a
n+1,则上述等式可以化为:b
n+2=2b
n+1+3b
n…(8分)
b
1=a
1+1=2,b
2=a
2+1=12,所以b
n+2=2b
n+1+3b
n对应的特征方程为:x
2-2x-3=0,x
1=-1,x
2=3…(10分)
所以令 b
n=c
1•3
n+c
2•(-1)
n,由b
1=2,b
2=12可以得出
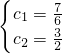
所以
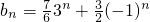
…(11分)
即
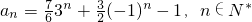
…(12分)
(3)同样可以得到通项公式

…(14分)
所以S
n=a
1C
n1+a
2C
n2+a
3C
n3+…+a
nC
nn=


=


=

即

…(14分)

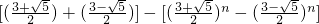
=3S
n+1-S
n即 S
n+2=3S
n+1-S
n,n∈N
*…(16分)
因此S
n+2除以8的余数,完全由S
n+1,S
n除以8的余数确定,
因为a
1=1,a
2=1所以 S
1=C
11a
1=1,S
2=C
21a
1+C
22a
2=3,S
3=3S
2-S
1=9-1=8,S
4=3S
3-S
2=24-3=21,S
5=3S
4-S
3=63-8=55,S
6=3S
5-S
4=165-21=144,S
7=3S
6-S
5=432-55=377,S
8=3S
7-S
6=1131-144=987,S
9=3S
8-S
7=2961-377=2584,
由以上计算及S
n+2=3S
n+1-S
n可知,数列{S
n}各项除以8的余数依次是:1,3,0,5,7,0,1,3,0,5,7,0,…,它是一个以6为周期的数列,从而S
n除以8的余数等价于n除以3的余数,所以n=3k,k∈N
*,
即所求集合为:{n|n=3k,k∈N
*}…(18分)
分析:(1)根据已知条件求出a
n+2=5a
n+1-6a
n的特征方程为:x
2-5x+6=0及其特征根x
1=2,x
2=3,利用待定系数法求出
c
1=c
2=1,进一步求出数列{a
n}的通项公式;
(2)先将已知条件变形为(a
n+2+1)=2(a
n+1+1)+3(a
n+1),设b
n=a
n+1,构造新数列{ b
n},通过求特征方程的特征根求出数列{ b
n}的通项公式,进一步求出数列{a
n}的通项公式;
(3)先通过求特征方程的特征根的方法求出通项公式

,代入S
n=a
1C
n1+a
2C
n2+…+a
nC
nn,化简得到 S
n+2=3S
n+1-S
n,通过不完全归纳找规律得到结论.
点评:本题考查通过题中的新定义求数列通项的方法,解决问题的关键是理解透题目中的新定义,在高考中场出现在小题中,本题属于难题.

 得到c1=c2=1,
得到c1=c2=1,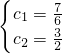
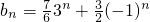 …(11分)
…(11分)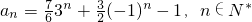 …(12分)
…(12分) …(14分)
…(14分)
 =
=
 =
=
 …(14分)
…(14分)
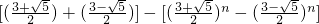 =3Sn+1-Sn
=3Sn+1-Sn ,代入Sn=a1Cn1+a2Cn2+…+anCnn,化简得到 Sn+2=3Sn+1-Sn,通过不完全归纳找规律得到结论.
,代入Sn=a1Cn1+a2Cn2+…+anCnn,化简得到 Sn+2=3Sn+1-Sn,通过不完全归纳找规律得到结论.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案