练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．“所有9的倍数的数都是3的倍数，5不是9的倍数，故5不是3的倍数．”上述推理（　　）
    A．是三段论推理，但大前提错B．是三段论推理，但小前提错
    C．不是三段论推理，但结论正确D．不是三段论推理，且结论不正确

    分析 “所有9的倍数的数都是3的倍数，5不是9的倍数，故5不是3的倍数．”上述推理不是三段论推理，但结论正确．

    解答 解：“所有9的倍数的数都是3的倍数，5不是9的倍数，故5不是3的倍数．”上述推理不是三段论推理，但结论正确，
    故选C．

    点评 本题是一个简单的演绎推理，这种问题不用进行运算，只要根据所学的知识点，判断这种说法是否正确，是一个基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知a＞0，b＞0且$\frac{1}{a}$+$\frac{2}{b}$=1，
    （1）求ab最小值；
    （2）求a+b的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

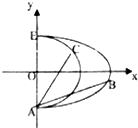    6．已知曲线C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0，x≥0）和曲线C2：x2+y2=r2（x≥0）都过点A（0，-1），且曲线C1所在的圆锥曲线的离心率为$\frac{\sqrt{3}}{2}$
    （1）求曲线C1，C2的方程
    （2）设点B，C分别在曲线C1，C2上，k1，k2分别为直线AB，AC的斜率，当k2=4k1时，
    ①直线BC是否经过定点？请说明理由
    ②设E（0，1），求|$\overrightarrow{BC}$|•|$\overrightarrow{BE}$|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若在区间[a，a+2]上，函数f（x）=2x-5的最小值不小于g（x）=4x-x2的最大值，则正数a的取值范围为（　　）
    A．[3，+∞）B．（0，3）C．（3，+∞）D．[3，4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+2y≥0}\\{x-y≤0}\\{x-2y+2≥0}\end{array}\right.$且a∈（-6，3），则z=$\frac{y}{x-a}$仅在点A（-1，$\frac{1}{2}$）处取得最大值的概率为（　　）
    A．$\frac{1}{9}$B．$\frac{2}{9}$C．$\frac{1}{3}$D．$\frac{4}{9}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数h（x）=$\left\{\begin{array}{l}{5-|x|（x≤5）}\\{（x-5）^{2}（x＞5）}\end{array}\right.$，函数φ（x）=m-h（5-x），其中m∈R，若函数：y=h（x）-φ（x）恰有4个零点，则m的取值范围是（　　）
    A．（5，+∞）∪{$\frac{19}{4}$}B．（$\frac{19}{4}$，5）C．（0，4）D．（-∞，$\frac{19}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下列命题正确的是（　　）
    A．若A，B，C是平面内的三点，则$\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{BC}$
    B．若$\overrightarrow{e_1}、\overrightarrow{e_2}$是两个单位向量，则$\overrightarrow{e_1}=\overrightarrow{e_2}$
    C．若$\overrightarrow a、\overrightarrow b$是任意两个向量，则$|{\overrightarrow a+\overrightarrow b}|≤|{\overrightarrow a}|+|{\overrightarrow b}|$
    D．向量$\overrightarrow{e_1}=（0，0），\overrightarrow{e_2}=（1，-2）$可以作为平面内所有向量的一组基底

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

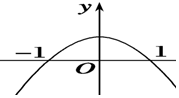    4．已知f′（x）是f（x）的导数，且y=xf′（x）的图象如图所示，则下列关于f（x）说法正确的是（　　）
    A．在（-∞，0）上是增函数B．在（-1，1）上是增函数
    C．在（-1，0）上是增函数D．在（1，+∞）上是减函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．函数f（x）=$\sqrt{{x^2}-1}+\sqrt{1-{x^2}}$是（　　）
    A．奇函数B．偶函数
    C．非奇非偶函数D．既是奇函数又是偶函数

    查看答案和解析>>

    同步练习册答案