
科目:高中数学 来源:2014-2015学年广东省惠州市高三4月模拟理科数学试卷(解析版) 题型:解答题
(本小题满分14分)如图,在四棱锥 中,底面
中,底面 为直角梯形,
为直角梯形, ,
, ,平面
,平面 ⊥底面
⊥底面 ,
, 为
为 的中点,
的中点, 是棱
是棱 上的点,
上的点, ,
, ,
, .
.

(1)求证:平面 ⊥平面
⊥平面 ;
;
(2)若二面角 为
为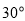 ,设
,设 ,试确定
,试确定  的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省忻州市高二上学期期末考试理科数学试卷(解析版) 题型:解答题
(本小题满分12分)在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 .
.
(1)求 的值;
的值;
(2)若 求
求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山西省忻州市高二上学期期末考试理科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,若输入x的值为2+log23,则输出y的值为( )
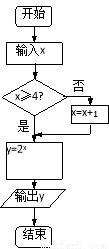
A.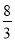 B.
B.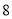 C.
C.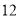 D.
D.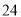
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江哈尔滨师大附中高二上学期期末考试理科数学卷(解析版) 题型:解答题
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程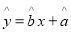 ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式: ,
,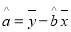 )
)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江哈尔滨师大附中高二上学期期末考试理科数学卷(解析版) 题型:选择题
已知 和
和 是两个分类变量,由公式
是两个分类变量,由公式 算出
算出 的观测值
的观测值 约为
约为
根据下面的临界值表可推断( )
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.推断“分类变量 和
和 没有关系”犯错误的概率上界为0.010
没有关系”犯错误的概率上界为0.010
B.推断“分类变量 和
和 有关系”犯错误的概率上界为0.010
有关系”犯错误的概率上界为0.010
C.有至少99%的把握认为分类变量 和
和 没有关系
没有关系
D.有至多99%的把握认为分类变量 和
和 有关系
有关系
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省温州市高三第二次适应性测试(二模)文科数学试卷(解析版) 题型:选择题
若某几何体的三视图(单位: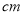 )如图所示,则此几何体的体积是( )
)如图所示,则此几何体的体积是( )
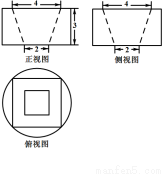
A.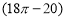
 B.
B.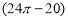
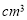
C.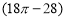
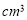 D.
D.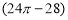
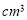
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省衢州市高三4月教学质量检测文科数学试卷(解析版) 题型:选择题
将函数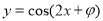 的图像沿
的图像沿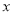 轴向右平移
轴向右平移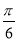 后,得到的图像关于原点对称,则
后,得到的图像关于原点对称,则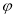 的
的
一个可能取值为( )
A.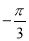 B.
B.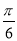 C.
C.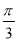 D.
D.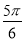
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com