
设f(x)=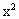 -bx+c且f(0)=3,f(1+x)=f(1-x).试比较
-bx+c且f(0)=3,f(1+x)=f(1-x).试比较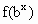 与
与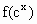 的大小.
的大小.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源:黄冈新内参·高考(专题)模拟测试卷·数学 题型:044
设f(x)=
 -bx+c,不等式f(x)<0解集是(-1,3)
-bx+c,不等式f(x)<0解集是(-1,3)
(1)若f(7+|t|)>f(1+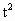 ),求实数t的取值范围;
),求实数t的取值范围;
(2)若 -2(a+b)的最小值为m,求
-2(a+b)的最小值为m,求
查看答案和解析>>
科目:高中数学 来源:2004年高考北京四中全真模拟试卷——数学 题型:013
设f(x)=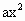 +bx+c(a≠0,α<β),则不等式f(α)·f(β)<0是方程f(x)=0在区间(α,β)内有且仅有一个实根的
+bx+c(a≠0,α<β),则不等式f(α)·f(β)<0是方程f(x)=0在区间(α,β)内有且仅有一个实根的
[ ]
|
A.充分条件 |
B.必要条件 |
|
C.充要条件 |
D.非充分非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com