
| A. | 3个 | B. | 2个 | C. | l个 | D. | 0个 |
分析 根据题意,将x1f(x1)+x2f(x2)≥x1f(x2)+x2f(x1)变形可得[f(x1)-f(x2)](x1-x2)≥0,进而分析可得若函数f(x)为“H函数”,则函数f(x)为增函数或常数函数;据此依次分析所给函数的单调性,综合可得答案.
解答 解:根据题意,对于x1f(x1)+x2f(x2)≥x1f(x2)+x2f(x1),
则有f(x1)(x1-x2)-f(x2)(x1-x2)≥0,
即[f(x1)-f(x2)](x1-x2)≥0,
分析可得:若函数f(x)为“H函数”,则函数f(x)为增函数或常数函数;
对于①、y=-x3+x+l,有y′=-3x2+l,不是增函数也不是常数函数,则其不是“H函数”,
对于②、y=3x-2(sinx-cosx);有y′=3-2(sinx+cosx)=3-2$\sqrt{2}$sin(x+$\frac{π}{4}$),有y′≥0,
y=3x-2(sinx-cosx)为增函数,则其是“H函数”,
对于③、y=l-ex=-ex+1,是减函数,则其不是“H函数”,
对于④、f(x)=$\left\{\begin{array}{l}{lnx(x≥1)}\\{0(x<1)}\end{array}\right.$,当x<1时是常数函数,当x≥1时是增函数,则其是“H函数”,
对于⑤、y=$\frac{x}{{x}^{2}+1}$,当x≠0时,y=$\frac{1}{x+\frac{1}{x}}$,当x>1和x<-1时,函数为减函数,故其不是增函数也不是常数函数,则其不是“H函数”,
综合可得:有2个是“H函数”,
故选:B.
点评 本题考查函数单调性的判定与应用,关键是依据x1f(x1)+x2f(x2)≥x1f(x2)+x2f(x1),判断出函数的单调性.


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
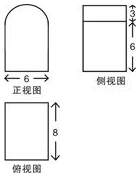 已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )
已知某几何体的三视图如图所示(正视图的弧线是半圆),根据图中标出的数据,这个几何体的表面积是( )| A. | 36π+288 | B. | 36π+216 | C. | 33π+288 | D. | 33π+216 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
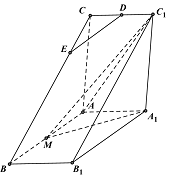 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com