
“―÷ΣΚ· ΐ Θ°Θ®
Θ°Θ® Θ©
Θ©
Θ®1Θ©»τ ‘Ύ«χΦδ
‘Ύ«χΦδ …œΒΞΒςΒί‘ωΘ§«σ Β ΐ
…œΒΞΒςΒί‘ωΘ§«σ Β ΐ ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®2Θ©»τ‘Ύ«χΦδ …œΘ§Κ· ΐ
…œΘ§Κ· ΐ ΒΡΆΦœσΚψ‘Ύ«ζœΏ
ΒΡΆΦœσΚψ‘Ύ«ζœΏ œ¬ΖΫΘ§«σ
œ¬ΖΫΘ§«σ ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨΫβΈωΓΩΒΎ“ΜΈ ÷–Θ§ Ήœ»άϊ”Ο ‘Ύ«χΦδ
‘Ύ«χΦδ …œΒΞΒςΒί‘ωΘ§‘ρ
…œΒΞΒςΒί‘ωΘ§‘ρ ‘Ύ«χΦδ
‘Ύ«χΦδ …œΚψ≥…ΝΔΘ§»ΜΚσΖ÷άκ≤Έ ΐΖ®ΒΟΒΫ
…œΚψ≥…ΝΔΘ§»ΜΚσΖ÷άκ≤Έ ΐΖ®ΒΟΒΫ Θ§ΫχΕχΒΟΒΫΖΕΈßΘΜΒΎΕΰΈ ÷–Θ§‘Ύ«χΦδ
Θ§ΫχΕχΒΟΒΫΖΕΈßΘΜΒΎΕΰΈ ÷–Θ§‘Ύ«χΦδ …œΘ§Κ· ΐ
…œΘ§Κ· ΐ ΒΡΆΦœσΚψ‘Ύ«ζœΏ
ΒΡΆΦœσΚψ‘Ύ«ζœΏ œ¬ΖΫΒ»Φέ”Ύ
œ¬ΖΫΒ»Φέ”Ύ ‘Ύ«χΦδ
‘Ύ«χΦδ …œΚψ≥…ΝΔΘ°»ΜΚσ«σΫβΒΟΒΫΓΘ
…œΚψ≥…ΝΔΘ°»ΜΚσ«σΫβΒΟΒΫΓΘ
ΫβΘΚΘ®1Θ© ‘Ύ«χΦδ
‘Ύ«χΦδ …œΒΞΒςΒί‘ωΘ§
…œΒΞΒςΒί‘ωΘ§
‘ρ ‘Ύ«χΦδ
‘Ύ«χΦδ …œΚψ≥…ΝΔΘ° Γ≠Γ≠Γ≠Γ≠3Ζ÷
…œΚψ≥…ΝΔΘ° Γ≠Γ≠Γ≠Γ≠3Ζ÷
Φ¥ Θ§ΕχΒ±
Θ§ΕχΒ± ±Θ§
±Θ§ Θ§Ι
Θ§Ι  Θ°
Γ≠Γ≠Γ≠Γ≠5Ζ÷
Θ°
Γ≠Γ≠Γ≠Γ≠5Ζ÷
Υυ“‘ Θ°
Γ≠Γ≠Γ≠Γ≠6Ζ÷
Θ°
Γ≠Γ≠Γ≠Γ≠6Ζ÷
Θ®2Θ©Νν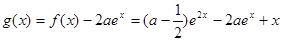 Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ Θ°
Θ°
‘Ύ«χΦδ …œΘ§Κ· ΐ
…œΘ§Κ· ΐ ΒΡΆΦœσΚψ‘Ύ«ζœΏ
ΒΡΆΦœσΚψ‘Ύ«ζœΏ œ¬ΖΫΒ»Φέ”Ύ
œ¬ΖΫΒ»Φέ”Ύ ‘Ύ«χΦδ
‘Ύ«χΦδ …œΚψ≥…ΝΔΘ°
…œΚψ≥…ΝΔΘ°
ΓΏ Γ≠Γ≠Γ≠Γ≠9Ζ÷
Γ≠Γ≠Γ≠Γ≠9Ζ÷
ΔΌ »τ Θ§Νν
Θ§Νν Θ§ΒΟΦΪ÷ΒΒψ
Θ§ΒΟΦΪ÷ΒΒψ Θ§
Θ§ Θ§
Θ§
Β± Θ§Φ¥
Θ§Φ¥ ±Θ§‘ΎΘ®
±Θ§‘ΎΘ® Θ§+Γό)…œ”–
Θ§+Γό)…œ”– Θ§¥Υ ±
Θ§¥Υ ± ‘Ύ«χΦδ
‘Ύ«χΦδ …œ «‘ωΚ· ΐΘ§≤Δ«“‘ΎΗΟ«χΦδ…œ”–
…œ «‘ωΚ· ΐΘ§≤Δ«“‘ΎΗΟ«χΦδ…œ”– Θ§≤ΜΚœΧβ“βΘΜ
Θ§≤ΜΚœΧβ“βΘΜ
Β± Θ§Φ¥
Θ§Φ¥ ±Θ§Ά§άμΩ…÷ΣΘ§
±Θ§Ά§άμΩ…÷ΣΘ§ ‘Ύ«χΦδ
‘Ύ«χΦδ …œΒί‘ωΘ§
…œΒί‘ωΘ§
”– Θ§“≤≤ΜΚœΧβ“βΘΜ
Γ≠Γ≠Γ≠Γ≠11Ζ÷
Θ§“≤≤ΜΚœΧβ“βΘΜ
Γ≠Γ≠Γ≠Γ≠11Ζ÷
ΔΎ »τ Θ§‘ρ”–
Θ§‘ρ”– Θ§¥Υ ±‘Ύ«χΦδ
Θ§¥Υ ±‘Ύ«χΦδ …œΚψ”–
…œΚψ”– Θ§¥”Εχ
Θ§¥”Εχ ‘Ύ«χΦδ
‘Ύ«χΦδ …œ «ΦθΚ· ΐΘΜ
…œ «ΦθΚ· ΐΘΜ
“Σ Ι ‘Ύ¥Υ«χΦδ…œΚψ≥…ΝΔΘ§÷Μ–κ¬ζΉψ
‘Ύ¥Υ«χΦδ…œΚψ≥…ΝΔΘ§÷Μ–κ¬ζΉψ
 Θ§
Θ§
”…¥Υ«σΒΟ ΒΡΖΕΈß «
ΒΡΖΕΈß « Θ° Γ≠Γ≠Γ≠Γ≠13Ζ÷
Θ° Γ≠Γ≠Γ≠Γ≠13Ζ÷
ΉέΚœΔΌΔΎΩ…÷ΣΘ§Β± ±Θ§Κ· ΐ
±Θ§Κ· ΐ ΒΡΆΦœσΚψ‘Ύ÷±œΏ
ΒΡΆΦœσΚψ‘Ύ÷±œΏ œ¬ΖΫΘ°
œ¬ΖΫΘ°
 –¬ΩΈ±ξΫΉΧί‘ΡΕΝ―ΒΝΖœΒΝ–¥πΑΗ
–¬ΩΈ±ξΫΉΧί‘ΡΕΝ―ΒΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| 2 | x |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| 1-x2 |
| 1+x |
| 1-x |
| 1+x |
| 1-x |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
| 1 | 2x+1 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com