练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知数列{an}中，a1=5且an=2an-1+2n-1(n≥2且n∈N*).

    (Ⅰ)证明：数列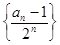为等差数列；

    (Ⅱ)求数列{ an-1}的前n项和Sn

     

    【答案】

    （1）数列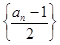为首项是2公差是1的等差数列.

    （2）Sn=n·2n+1

    【解析】(1)根据等差数列的定义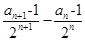是定值即可.

    (2)在第（I）问的基本上求出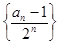的通项公式，进而求出{ an-1}的通项公式,然后根据数列求和的方法求值即可。

    解：(Ⅰ)设bn=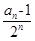, b1=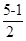=2      ……………………………………………1分

    bn+1- bn=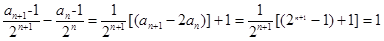  …4分

       所以数列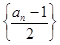为首项是2公差是1的等差数列.      …………………………5分

        (Ⅱ)由(Ⅰ)知，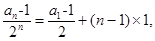

        ∴an-1=(n+1)·2n          …………………………7分

        ∵Sn=2·21+3·22+…+n·2n-1+(n+1)·2n         ①

    ∴2Sn=2·22+3·23+…+ n·2n+(n+1)·2n+1             ②……………………9分

    ①—②，得 - Sn=4+（22+23+…+2n）-(n+1)·2n+1

    ∴Sn=-4-4（2n+1-1）+(n+1)·2n+1  

    ∴Sn=n·2n+1 

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知数列{an}中，a1=1，an+1-an=
    1
    3n+1
    (n∈N*)    ，则
    lim
    n→∞
    an    =
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}中，a1=1，an+1=
    an
    1+2an
    ，则{an}的通项公式an=
    1
    2n-1
    1
    2n-1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}中，a1=1，a1+2a2+3a3+…+nan=
    n+1
    2
    an+1(n∈N*)    ．
    （1）求数列{an}的通项公式；
    （2）求数列{
    2n
    an
    }    的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}中，a1=
    1
    2
    ，Sn    为数列的前n项和，且Sn与
    1
    an
    的一个等比中项为n(n∈N*    ），则
    lim
    n→∞
    Sn    =
    1
    1
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知数列{an}中，a1=1，2nan+1=（n+1）an，则数列{an}的通项公式为（　　）
    A、
    n
    2n
    B、
    n
    2n-1
    C、
    n
    2n-1
    D、
    n+1
    2n

    查看答案和解析>>

    同步练习册答案