

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:
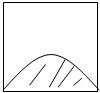 如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是
如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为
(2013•枣庄二模)如图所示,墙上挂有一块边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的扇形.某人向此木板投镖,假设每次都能击中木板,且击中阴影部分的概率为| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
查看答案和解析>>
科目:高中数学 来源:2013年山东省枣庄市高考数学二模试卷(文科)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com