Question

边长均大于l的矩形面积为3，若其长和宽各减少1，则所得新的矩形面积的最大值是________．

Answer 1

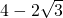
分析：设原来矩形的长和宽分别为a，b（a＞1，b＞1），且ab=3，设新矩形的面积为S，则S=（a-1）（b-1）=ab-（a+b）+1=4-（a+b）
由基本不等式可求
解答：设原来矩形的长和宽分别为a，b（a＞1，b＞1），且ab=3
设新矩形的面积为S，则S=（a-1）（b-1）=ab-（a+b）+1=4-（a+b）
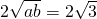
a+b≥，当且仅当a=b=时取等号
∴
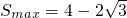
故答案为：．
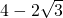
点评：本题主要考查了利用基本不等式在积定求和的最小值的应用，属于基础试题．