
分析 (1)利用平行四边形的性质、中点坐标公式即可得出.
(2)利用垂直平分线的性质即可得出;
(3)利用两点之间的距离公式、点到直线的距离公式、三角形面积计算公式即可得出.
解答 解:(1)设AC中点为M,则$M(\frac{3}{2},2)$
由ABCD为平行四边形知M为BD中点,而B(3,2)
故D(0,2).
(2)直线AB方程为y=x-1
过点C且与AB垂直的直线方程为y=-x+6,
由$\left\{\begin{array}{l}y=x-1\\ y=-x+6\end{array}\right.$,得交点E为$({\frac{7}{2},\frac{5}{2}})$,
设点C关于直线AB的对称点为C′,
则E为C,C′的中点,故C′点坐标为(5,1).
(3)$AB=\sqrt{{{(1-3)}^2}+{{(0-2)}^2}}=2\sqrt{2}$,
点C(2,4)到直线AB:x-y-1=0的距离为$d=\frac{|2-4-1|}{{\sqrt{2}}}=\frac{{3\sqrt{2}}}{2}$,
∴${S_{△ABC}}=\frac{1}{2}×2\sqrt{2}×\frac{{3\sqrt{2}}}{2}=3$.
点评 本题考查了平行四边形的性质、中点坐标公式、垂直平分线的性质、两点之间的距离公式、点到直线的距离公式、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$) | D. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
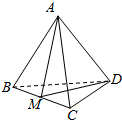 如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )
如图所示的正四面体A-BCD中,截面ADM将其分成体积相等的两部分,则AB与截面ADM所成角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 无法确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com