
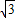 则△ABC的边长AC是( )
则△ABC的边长AC是( )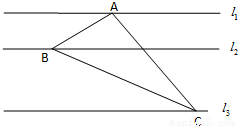
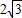
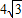
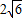
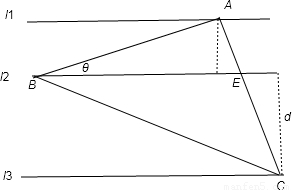
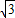 x,(x>0),设AC与l2的交点为E,由条件易得∠ABC=90°,设∠ABE=θ,则∠CBE=60°-θ,则可得sinθ=sin(60°-θ),则有θ=30°,从而可求AE,EC,在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE,代入可求x,进而可求AC
x,(x>0),设AC与l2的交点为E,由条件易得∠ABC=90°,设∠ABE=θ,则∠CBE=60°-θ,则可得sinθ=sin(60°-θ),则有θ=30°,从而可求AE,EC,在Rt△ABE中,由三角形的面积公式可得,AB•AE=2BE,代入可求x,进而可求AC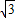 x,(x>0),设AC与l2的交点为E
x,(x>0),设AC与l2的交点为E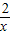 ,
,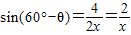
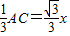 ,EC=
,EC=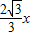 =BE
=BE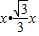 =
=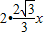



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 求
求| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图11,12,13是同一平面内的三条平行直线,11与12间的距离是2,12与l3间的距离是4.三角形ABC的三个顶点分别在l1、l2、l3上,且三边AB,BC,AC的长之比为1:2:
如图11,12,13是同一平面内的三条平行直线,11与12间的距离是2,12与l3间的距离是4.三角形ABC的三个顶点分别在l1、l2、l3上,且三边AB,BC,AC的长之比为1:2:| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com