
 (I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
(I)求该小组中女生的人数; (II)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为 ,每个男生通过的概率均为
,每个男生通过的概率均为 ,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
,现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量 ,求
,求 的分布列和数学期望。
的分布列和数学期望。 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立. ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题



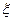 为甲、乙、丙这三个学生参加A社团的人数,求
为甲、乙、丙这三个学生参加A社团的人数,求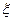 的分布列与
的分布列与
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分 . 现从盒内任取3个球.
分 . 现从盒内任取3个球. 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张.
,若中奖,商场返回顾客现金100元.某顾客现购买价格为2300的台式电脑一台,得到奖券4张. ,求
,求 的分布列;
的分布列; (元),用
(元),用 表示
表示 ,并求
,并求 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
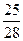 ,请你回答有几张“奥运会徽” 卡呢?
,请你回答有几张“奥运会徽” 卡呢?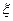 表示4人中的某人获奖终止游戏时总共抽取卡片的次数,求
表示4人中的某人获奖终止游戏时总共抽取卡片的次数,求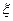 的数学期望。
的数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.0.18 | B.0.20 | C.0.14 | D.0.16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com