练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某空间组合体的三视图如图所示,则该组合体的体积为(　)

    (A)48   (B)56   (C)64   (D)72


    　C解析:该组合体由两个棱柱组成,上面的棱柱体积为2×4×5=40,下面的棱柱体积为4×6×1=24,

    故组合体的体积为64.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    咖啡馆配制两种饮料,甲种饮料每杯含奶粉9克、咖啡4克、糖3克,乙种饮料每杯含奶粉4克、咖啡5克、糖10克.已知每天原料的使用限额为奶粉3600克、咖啡2000克、糖3000克,甲种饮料每杯能获利润0.7元,乙种饮料每杯能获利润1.2元,每天应配制两种饮料各多少杯能获利最大?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则中最大的是           .

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于(　 　)

    (A)1    (B)  

    (C)  (D)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为(　　)

    (A)6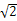  (B)4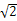  (C)6    (D)4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知正三角形ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是(　　)

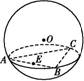
     (A)π (B)2π  (C)π  (D)3π

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若三棱锥SABC的所有顶点都在球O的球面上,SA⊥平面ABC,SA=2,AB=1,AC=2,∠BAC=60°,则球O的表面积为　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图,已知:E,F,G,H分别是正方体ABCDA1B1C1D1的棱AB,BC,CC1,C1D1的中点,证明:EF,HG,DC三线共点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若向量a=(1,λ,2),b=(2,-1,2)且a与b的夹角的余弦值为,则λ=　　　　. 

    查看答案和解析>>

    同步练习册答案