
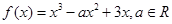
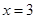 是
是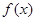 的极值点,求
的极值点,求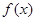 在
在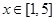 上的最大值
上的最大值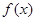 是R上的单调递增函数,求实数的
是R上的单调递增函数,求实数的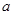 的取值范围.
的取值范围. 时,函数
时,函数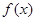 有最大值为15. (2)
有最大值为15. (2) 。
。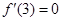 可求出a的值,从而再求出极值,与区间的端点值比较可求出最大值.
可求出a的值,从而再求出极值,与区间的端点值比较可求出最大值.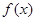 是R上的单调递增函数可转化为
是R上的单调递增函数可转化为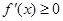 在R上恒成立问题来解决.
在R上恒成立问题来解决.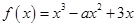 ,
,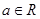 ,且当
,且当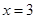 时有极值.
时有极值.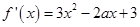 ---------------------- 1分
---------------------- 1分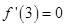 所以
所以 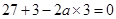
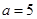 -------- 2分
-------- 2分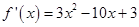 ------------------------- 3分
------------------------- 3分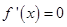 时,
时,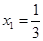 ,
,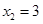
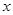 | 1 | 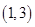 | 3 | 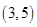 | 5 |
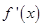 | | — | 0 | + | |
 | -1 | 单调递减 | 极小值 | 单调递增 | 15 |
 时,函数
时,函数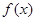 有最大值为15. ------------------------------ 6分
有最大值为15. ------------------------------ 6分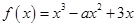 为在
为在 上的单调递增函数
上的单调递增函数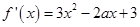 所以
所以 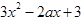 ≥0在R上恒成立,
≥0在R上恒成立,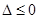 ------------------------- 8分
------------------------- 8分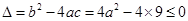 ---------
---------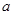 的取值范围是
的取值范围是  ------------------ 12 分
------------------ 12 分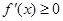 在R上恒成立.
在R上恒成立.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com