直线y=mx+1与椭圆ax2+y2=2交于A,B两点,以OA,OB为邻边作平行四边形OAPB(O为坐标原点).
(1)若a=2,求点P的轨迹方程;
(2)若a,m满足a+2m2=1,求平行四边形OAPB的面积函数S(a)的值域.
【答案】
分析:(1)直线y=mx+1过定点(0,1),设A(x
1,y
1),B(x
2,y
2),则OP的中点M为
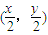
,且有2x
12+y
12=2,2x
22+y
22=2,由此能求出点P的轨迹方程.
(2)由
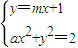
,得(a+m
2)x
2+2mx-1=0,所以
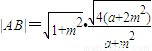
,再由点O到AB的距离
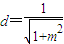
,能求出S(a)的值域.
解答:解:(1)直线y=mx+1过定点(0,1),
设A(x
1,y
1),B(x
2,y
2),
则OP的中点M为
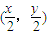
,
且有2x
12+y
12=2,2x
22+y
22=2,
以上两式相减,得
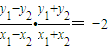
,
即k
AB•k
OP=-2,
∴
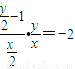
,
∴2x
2+y
2-2y=0,
点P的轨迹方程为2x
2+(y-1)
2=1(除去原点).
(2)由
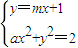
,
得(a+m
2)x
2+2mx-1=0,
∴
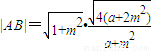
,
又点O到AB的距离
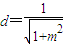
,
∴
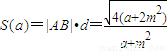
=
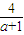
.
∵a+2m
2=1,
∴0<a<1,
∴S(a)的值域为(2,4).
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

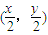 ,且有2x12+y12=2,2x22+y22=2,由此能求出点P的轨迹方程.
,且有2x12+y12=2,2x22+y22=2,由此能求出点P的轨迹方程.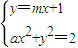 ,得(a+m2)x2+2mx-1=0,所以
,得(a+m2)x2+2mx-1=0,所以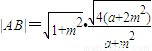 ,再由点O到AB的距离
,再由点O到AB的距离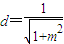 ,能求出S(a)的值域.
,能求出S(a)的值域.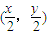 ,
,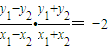 ,
,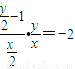 ,
,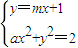 ,
,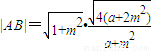 ,
,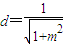 ,
,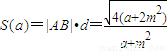 =
=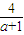 .
.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案