
已知a>1, = log
= log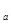 (a-a
(a-a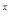 ).
).
⑴ 求 的定义域、值域;
的定义域、值域;
⑵判断函数 的单调性 ,并证明;
的单调性 ,并证明;
⑶解不等式: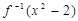 >
> .
.
⑴定义域为(-∞,1); 值域为(-∞,1)
⑵函数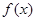 为减函数,证明见解析
为减函数,证明见解析
⑶不等式的解为-1<x<1
【解析】为使函数有意义,需满足a-a >0,即a
>0,即a <a,当注意到a>1时,所求函数的定义域为(-∞,1),
<a,当注意到a>1时,所求函数的定义域为(-∞,1),
又log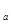 (a-a
(a-a )<log
)<log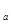 a = 1,故所求函数的值域为(-∞,1).
a = 1,故所求函数的值域为(-∞,1).
⑵设x <x
<x <1,则a-a
<1,则a-a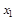 >a-a
>a-a ,所以
,所以 -
-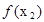 = log
= log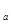 (a-a
(a-a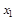 )-log
)-log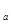 (a-a
(a-a )>0,即
)>0,即 >
>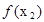 .
.
所以函数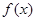 为减函数.
为减函数.
⑶易求得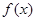 的反函数为
的反函数为 = log
= log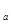 (a-a
(a-a )
(x<1),
)
(x<1),
由 >
>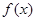 ,得log
,得log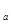 (a-a
(a-a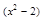 )>log
)>log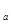 (a-a
(a-a ),
),
∴a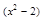 <a
<a ,即x
,即x -2<x,解此不等式,得-1<x<2,
-2<x,解此不等式,得-1<x<2,
再注意到函数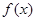 的定义域时,故原不等式的解为-1<x<1.
的定义域时,故原不等式的解为-1<x<1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:044
已知f (x)=lo ga![]() (a>0,a≠1).
(a>0,a≠1).
(Ⅰ)求f (x)的定义域;
(Ⅱ)判断f (x)的奇偶性并予以证明;
(Ⅲ)求使f (x)>0的x取值范围.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(Ⅰ)求f (x)的定义域;
(Ⅱ)判断f (x)的奇偶性并予以证明;
(Ⅲ)求使f (x)>0的x取值范围.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:013
(A) a<b<c (B) a<c<b (C) c<b<a (D) c<a<b
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:2.8 对数与对数函数(解析版) 题型:解答题
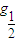 [a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?
[a2x+2(ab)x-b2x+1](a、b∈R+),如何求使y为负值的x的取值范围?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com