Question

已知点A(3,0)、B(0,3)、C(cosα,sinα),α∈().

(1)若||=||,求角α的值;

(2)(理)若=-1,求的值.

(文)若()·=2(O是坐标原点),求的值.

Answer 1

解:(1)方法一:∵A(3,0)、B(0,3)、C(cosα,sinα),

∴=(cosα-3,sinα),=(cosα,sinα-3).                                        

由||=||,得,

即cosα=sinα.                                                              

∵＜α＜,∴α=.                                                     

方法二:∵||=||,

∴点C在直线y=x上.                                                       

则sinα=cosα.                                                               

∵α∈(),∴α=.                                                    

(2)(理)

=2sinαcosα.                                                                

由=-1,得

(cosα-3)cosα+sinα(sinα-3)=-1,                                                

即sinα+cosα=.

∴(sinα+cosα)²=1+2sinαcosα=,

即2sinαcosα=.                                                       

∴.                                                

(文)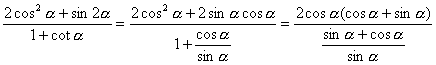

=2sinαcosα.                                                               

由()·=2,

得sinα+cosα=.                                                          

∴(sinα+cosα)²=1+2sinαcosα=,

即2sinαcosα=.

∴.